| netlib.narod.ru | < Назад | Оглавление | Далее > |
Простите меня. Я знаю, что на обложке книги ни слова не сказано о том, что вам придется заниматься геометрией, но перед тем, как создавать собственные фигуры, необходимо познакомиться с терминологией и посмотреть, какие законы действуют в трехмерном мире. Для начала еще раз взглянем на систему координат.
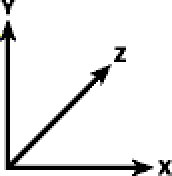
В механизме визуализации используется левосторонняя система координат (разумеется, проницательный читатель поднимает левую руку и вертит пальцами, показывая, куда направлены оси X, Y и Z). Если же вы проспали весь разговор о системах координат в главе 1, посмотрите на рис. 4.1 — на нем изображена левосторонняя система, которой мы будем пользоваться.

Рис. 4.1. Левосторонняя система координат
Положительная часть оси Y направлена вверх, X — вправо, а Z — в глубь экрана, от пользователя.
Разобравшись с направлениями осей, следует договориться о единицах измерения для создаваемых объектов. Единицы измерения — понятие условное. Например, можно измерять размеры создаваемых объектов в километрах. Возможно, это звучит нелепо, но если отодвинуть камеру на несколько километров от таких гигантских объектов, вид будет вполне нормальным — в нашем трехмерном мире нет загрязнения воздуха, которое бы могло испортить картину.
Давайте ненадолго отвлечемся от темы. Знаете ли вы, что одна из проблем, возникавших у астронавтов при выходе в космос, как раз и заключалась в том, что им не удавалось нормально оценить размеры объектов и расстояния до них? Дело в том, что интенсивность света, проходящего через космический вакуум, остается постоянной (тогда как в земной атмосфере свет рассеивается). Следовательно, объекты в космосе выглядят исключительно четко, даже если они удалены от вас на многие километры. Интересно, правда? Так и хочется обратиться в NASA и записаться на курсы астронавтов.
Аналогичные проблемы возникают и с нашими фигурами, поскольку их размер на экране зависит только от размеров объектов и их расстояния от камеры. Остается лишь произвольно задать положение камеры и по нему определить, какими должны быть размеры объектов. В создаваемых нами макетах камера по умолчанию находится в 10 единицах от начала координат, то есть в точке с координатами 0, 0, –10. Объект размером в 1 единицу (скажем, куб с единичным ребром), находящийся в начале координат (0, 0, 0), при стандартном расположении камеры смотрится на экране вполне нормально. Следовательно, длина, ширина и высота создаваемых нами объектов обычно должна составлять несколько единиц.
Поскольку мы пользуемся координатами с плавающей точкой, работа с численно малыми единицами не приведет к потере точности. Ситуация в корне отличается от манипуляций с целыми числами, которые нельзя бесконечно делить на меньшие части. На рис. 4.2 снова изображены оси, но на этот раз на них нанесены примерные значения координат, которыми мы будем пользоваться.
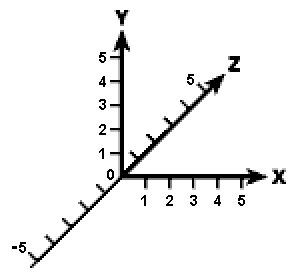
Рис. 4.2. Оси координат в типичном масштабе
Зная, куда направлены оси и где находятся наши объекты, можно приступать к созданию точек, определяющих внешний вид объекта.
Давайте нарисуем собачку. Возьмите карандаш и соедините точки на рис. 4.3, начиная с точки 1 и следуя по порядку чисел.
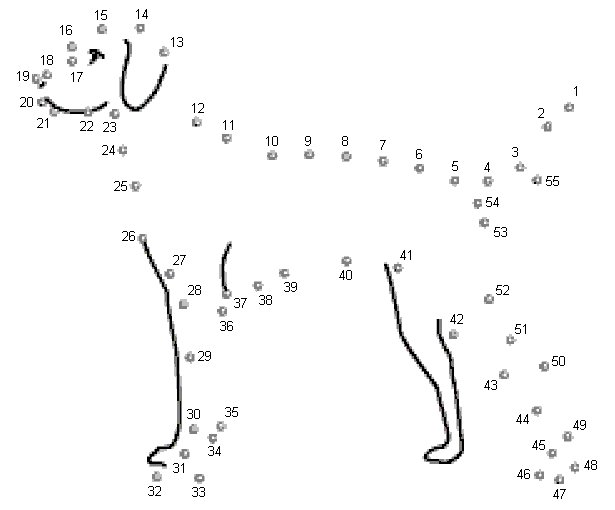
Рис. 4.3. Соедините точки
— Папа, что ты делаешь?
— Изучаю работу механизма визуализации для компьютерной трехмерной графики.
— Как просто — я так тоже могу.
У нас получилась плоская, двумерная собака, но вы наверняка уловили общий принцип: указывая, в каком порядке следует соединять точки, можно определить довольно сложную фигуру. В геометрии такие точки называются вершинами, и в дальнейшем мы будем именовать их именно так. Вершина является точкой пересечения нескольких отрезков, причем нас будут интересовать только прямые отрезки (я уверен, что вы соединили точки на рисунке плавными кривыми; если же вы соединяли их отрезками прямых, то вы наверняка прославитесь в мире компьютерной графики, но про рисование собак вам лучше забыть). Разумеется, если картинка будет состоять из очень большого количества точек, то даже настоящий тупица, соединяя точки по линейке, нарисует вполне приличную собаку.
Так в чем же суть всех наших рассуждений о собаках и точках? Дело в том, что компьютер умеет рисовать только прямые линии. Если мы захотим создать криволинейную фигуру, придется либо составлять ее из множества вершин, либо изобретать какой-нибудь другой способ для улучшения ее внешнего вида. Мы еще вернемся к рисованию криволинейных фигур в разделе «Создание твердых тел». А пока достаточно запомнить на будущее определение вершин.
Для определения вектора в трехмерном пространстве необходимо указать три координаты: x, y и z. Началом координат нашей системы является точка 0, 0, 0. Рассмотрим точку в левом верхнем углу (и немного в глубь экрана), которая имеет координаты –2, 3, 4. Чтобы определить положение вершины, можно задать вектор, направленный из начала координат в точку трехмерного пространства. На рис. 4.4 изображен вектор, который определяет точку с координатами –2, 3, 4.
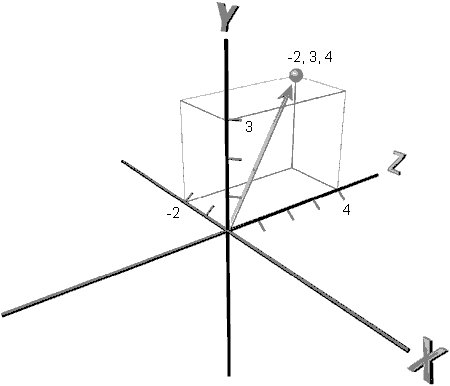
Рис. 4.4. Вектор, определяющий точку –2, 3, 4
Кроме того, с помощью вектора можно определить направление. Например, вектор 0, 1, 0 определяет верхнее, то есть положительное направление оси Y (рис. 4.5).

Рис. 4.5. Вектор, определяющий направление
В тех случаях, когда вектор используется для определения направления, его длина не имеет значения. Если хотя бы одна из координат вектора отлична от нуля, такой вектор однозначно задает направление. Тем не менее для определения направлений принято пользоваться единичными векторами. Длина единичного вектора равна 1, то есть:
x2+y2+z2 = 1
При написании программы часто бывает нежелательно вычислять точные значения координат, при которых данный вектор становится единичным, поэтому обычно существует какое-нибудь средство для нормирования векторов (то есть приведения их к единичной длине). Класс C3dVector содержит функцию Normalize, которая выполняет эту задачу. Почему желательно задавать направление единичным вектором? При изменении ориентации объекта, единичные векторы упрощают вычисления с вершинами объекта. Тем не менее, вызывая функции механизма визуализации, вы не обязаны передавать им единичные векторы, поскольку перед использованием вектора он автоматически нормируется. Необходимость нормирования возникает только при проведении ваших собственных вычислений с векторами (другое распространенное применение единичных векторов заключается в определении нормали к плоскости; см. раздел «Нормали»).
Но довольно о векторах. Давайте подведем итог: вектор может определять положение вершины или направление.
Для того чтобы однозначно задать положение и ориентацию трехмерного объекта в пространстве, необходимы три вектора. Первый вектор определяет положение объекта (или, по крайней мере, некоторой эталонной точки объекта). Второй вектор определяет направление, в котором обращен объект. Для чего же нужен третий вектор? На рис. 4.6 изображены три объекта, все они имеют одинаковую форму и обращены в одном направлении. Чем они отличаются друг от друга?
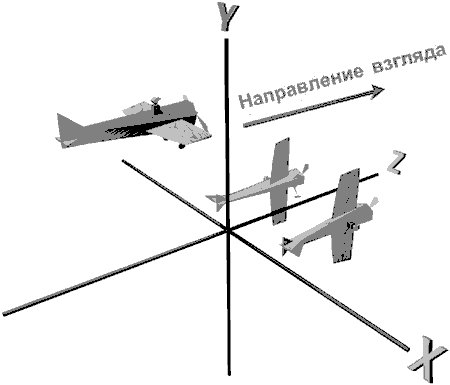
Рис. 4.6. Три объекта, обращенные в одном направлении
Отличие состоит в том, что все эти объекты повернуты на разный угол вокруг своей оси. Чтобы полностью задать ориентацию объекта, необходимо дополнительно определить направление, которое для объекта будет считаться верхним. На рис. 4.7 изображены верхние векторы для всех трех фигур.

Рис. 4.7. Для окончательного определения ориентации объекта необходимо задать верхние векторы
Три вектора однозначно определяют позицию и ориентацию объекта.
В нарисованной вами собачке (рис. 4.3) множество вершин использовалось для определения одной грани неправильной формы. Трехмерные объекты состоят из нескольких граней, причем для компьютера эти грани являются абсолютно плоскими. Чтобы изобразить «гладкую» сферу, потребуется довольно много плоских граней. Грани могут иметь любую форму — от простейших треугольников до сложных многоугольников, так что вам удастся собрать свой трехмерный объект из треугольников, квадратов, пятиугольников и вообще из любых фигур.
Следует учесть, что независимо от заданной формы граней механизм визуализации во время рисования обычно разбивает многоугольные грани на треугольники. Конечно, если в вашем компьютере установлена какая-нибудь сверхмощная видеокарта вместе с такими же мощными драйверами, она может обойтись без деления и рисовать многоугольники непосредственно на аппаратном уровне. Вы спросите, какое это имеет значение? Если вы захотите построить свою фигуру из каких-нибудь особенных многоугольников, чтобы сократить количество граней и тем самым ускорить ее прорисовку, возможно, разумнее с самого начала собирать ее из треугольников или других многоугольников с более простой формой — все равно ваш компьютер воспроизводит грани как совокупности треугольников. Кроме того, иногда это может приводить к довольно неожиданным эффектам. Если просто задать вершины многоугольника и воспроизвести его в окне, ваш «плоский» многоугольник может обрасти треугольными выступами. Причины такого явления мы рассмотрим чуть позже, в разделе «Создание простых фигур». А пока попробуем построить наши объекты из треугольников и квадратов и посмотрим, что получится.
Последнее, о чем следует помнить — при задании вершин, определяющих грань, необходимо перечислять их по часовой стрелке (рис. 4.8). Это очень важно, поскольку механизм визуализации воспроизводит только одну сторону грани. Ограничиваясь лишь передней поверхностью граней, механизм визуализации избавляется от необходимости рисовать невидимые грани и тем самым экономит время. Будьте внимательны при задании вершин грани и следите за тем, чтобы грань была видна с нужной стороны.
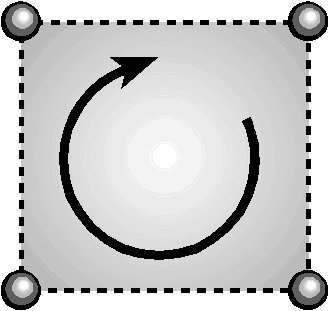
Рис. 4.8. Порядок обхода вершин грани
Разумеется, для создания нужной фигуры вершины граней также необходимо перечислять в правильном порядке. Нельзя наугад указать шесть-семь вершин и надеяться на то, что механизм визуализации как-нибудь соберет их в одну грань. Если в нашем примере вы не будете соединять точки по порядку, то получится не милая собачка, а сплошное безобразие.
Нормалями называют людей, которые не станут заниматься геометрией ради собственного развлечения. Конечно, это шутка — например, я люблю геометрию, но при этом вполне нормален (я уверен в этом, потому что мне так говорили окружающие — честное слово!). Так что же такое нормаль?
Нормалью (по отношению к грани) называется вектор, определяющий ориентацию грани. На рис. 4.9 изображена грань вместе с нормалью к ней.
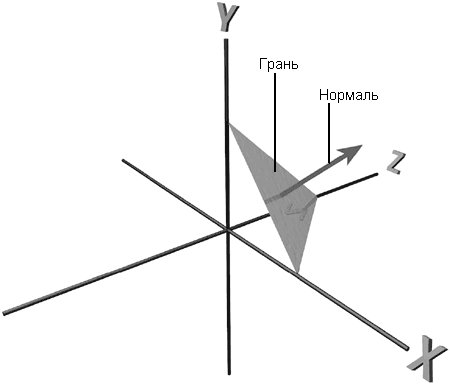
Рис. 4.9. Грань и нормаль
Нормалью грани является вектор, перпендикулярный ее поверхности. Для чего же нужны нормали? Знание ориентации граней может пригодиться при наложении текстур на объект. По нормалям можно определить, как следует ориентировать текстуру для достижения желаемого эффекта. На данный момент это несущественно, поэтому давайте рассмотрим другое применение нормалей.
В некоторых методах трехмерной визуализации закраска грани зависит от направления ее нормали и расположения источников света в макете. Подобная закраска равномерно окрашивает грань и придает ей плоский вид. Поскольку большинство объектов в нашей жизни все же имеет объем, несколько плоских граней еще не дают иллюзии реальности. Любой художник покажет вам, как правильно наложенные тени на плоском листе бумаги создают иллюзию реального, твердого объекта. Следовательно, при разумном наложении теней на грани наших трехмерных объектов можно получить более реалистичные изображения. Именно здесь нужны нормали.
Механизм визуализации, с которым мы работаем, поддерживает несколько режимов закраски, однако для своих приложений я выбрал закраску методом Гуро (названную по фамилии автора). В этой методике закраска грани определяется направлением нормалей в ее вершинах.
Предположим, у нас имеется прямоугольная грань и с каждой ее вершиной связан вектор нормали, как показано на рис. 4.10.

Рис. 4.10. Грань с нормалями вершин
На рис. 4.10 все нормали обращены вертикально вверх. При закраске по методу Гуро такая грань будет выглядеть плоской, так как все нормали вершин обращены в одном и том же направлении, и потому все точки грани, расположенные между вершинами, будут освещены одинаково. Возможно, это покажется вам неочевидным и даже непонятным, но давайте попробуем представить себе, что нормали определяют, насколько плоской выглядит грань у вершин. На рис. 4.10 все векторы направлены одинаково, поэтому вся грань выглядит плоской. Соответственно, ее освещенность остается постоянной.
Изменим положение нормалей и посмотрим, к каким последствиям это приведет. На рис. 4.11 изображена та же самая грань с другими, неперпендикулярными нормалями.

Рис. 4.11. Грань с неперпендикулярными нормалями
При освещении такая грань выглядит вогнутой, поскольку направления нормалей изменяются от вершины к вершине так, что углы словно приподнимаются над плоскостью грани.
Если вы ничего не поняли, не огорчайтесь — сейчас мы продемонстрируем сказанное на примере программы, и тогда все станет гораздо понятнее.
| netlib.narod.ru | < Назад | Оглавление | Далее > |