Создание твердых тел

Довольно об отдельных гранях! Давайте немного изменим нашу программу и создадим куб:

void CMainFrame::OnEditDefcube()
{
    D3DVECTOR vlist [] = {
        {-1, -1, -1},
        {-1, -1,  1},
        { 1, -1,  1},
        { 1, -1, -1},
        {-1,  1, -1},
        {-1,  1,  1},
        { 1,  1,  1},
        { 1,  1, -1}
    };
    int nv = sizeof(vlist) / sizeof(D3DVECTOR);

    int flist [] = {4, 0, 3, 2, 1,
                    4, 3, 7, 6, 2,
                    4, 4, 5, 6, 7,
                    4, 0, 1, 5, 4,
                    4, 0, 4, 7, 3,
                    4, 2, 6, 5, 1,
                    0
    };
    NewScene();
    m_pShape = new C3dShape;
    m_pShape->Create(vlist, nv, flist);
    m_pScene->AddChild(m_pShape);
} 

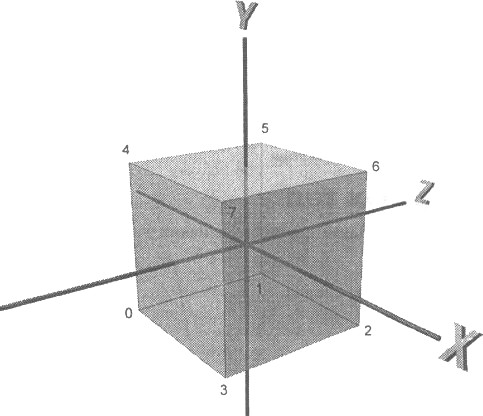
Список вершин теперь состоит из восьми элементов, по одному для каждого из углов куба, а список граней содержит шесть элементов по числу граней куба. На рис. 4.15 изображен куб с пронумерованными вершинами, он поможет вам понять значения элементов списка данных граней в приведенном выше фрагменте. Следует помнить о том, что вершины каждой грани должны перечисляться по часовой стрелке относительно того направления, с которого будет видна данная грань.

Рис. 4.15. Нумерация вершин куба

Прежде, чем читать дальше, следует самостоятельно убедиться в том, что вы поняли смысл описания граней. Может, на это придется потратить немного времени, зато в дальнейшем вы не будете создавать невидимые поверхности, ориентированные в неверном направлении. Функция OnEditDefcube строит фигуру, изображенную на рис. 4.16. Чтобы увидеть куб на экране, выполните команду Edit | Default Cube.

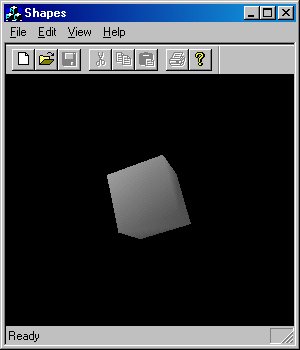
Рис. 4.16. Вращающийся куб с принятым по умолчанию расположением нормалей

Как вы думаете, почему закраска граней выглядит такой однородной? Выполните команду View | Normals, и вы увидите, что нормали к вершинам куба обращены от углов, по направлению от центра куба. Поскольку мы не стали задавать свои нормали, механизм визуализации создал их по умолчанию, усредняя нормали всех граней, прилегающих к вершине. Подобное решение может показаться довольно странным, особенно при создании куба. Тем не менее оно выглядит вполне разумно при создании сферы или другой криволинейной фигуры, поскольку усредненные нормали помогают создать более реалистичный объект — закраска сглаживает края прилегающих граней.

Разумеется, мы все же рассчитывали увидеть другой куб, с плоскими гранями и четко различимыми ребрами. Для того чтобы решить эту проблему, достаточно определить свои собственные нормали. Для вершин каждой грани мы задаем нормали, направление которых совпадает с нормалью грани. Приведенная ниже функция создает куб с плоскими гранями:

void CMainFrame::OnEditFlatfacecube()
{
    D3DVECTOR vlist [] = {
        {-1, -1, -1},
        {-1, -1,  1},
        { 1, -1,  1},
        { 1, -1, -1},
        {-1,  1, -1},
        {-1,  1,  1},
        { 1,  1,  1},
        { 1,  1, -1}
    };
    int nv = sizeof(vlist) / sizeof(D3DVECTOR); 

    D3DVECTOR nlist [] = {
        { 1,  0,  0},
        { 0,  1,  0},
        { 0,  0,  1},
        {-1,  0,  0},
        { 0, -1,  0},
        { 0,  0, -1}
    };
    int nn = sizeof(nlist) / sizeof(D3DVECTOR);
    int flist [] = {4, 0, 4, 3, 4, 2, 4, 1, 4,
                    4, 3, 0, 7, 0, 6, 0, 2, 0,
                    4, 4, 1, 5, 1, 6, 1, 7, 1,
                    4, 0, 3, 1, 3, 5, 3, 4, 3,
                    4, 0, 5, 4, 5, 7, 5, 3, 5,
                    4, 2, 2, 6, 2, 5, 2, 1, 2,
                    0
    }; 

    NewScene();
    m_pShape = new C3dShape;
    m_pShape->Create(vlist, nv, nlist, nn, flist);
    m_pScene->AddChild(m_pShape);
}

Если запустить приложение и отобразить куб с плоскими гранями вместе с нормалями (сначала выполните команду Edit | Flat Faced Cube, затем — команду View | Normals), вы увидите нечто похожее на рис. 4.17.

Рис. 4.17. Куб с плоскими гранями и векторами нормалей

Итак, теперь мы умеем создавать фигуры с плавными переходами граней (при которых нормали генерируются механизмом визуализации) или с более резкими переходами (при которых нормали задаются программистом). Иногда бывает нужно создать криволинейный объект, на котором присутствуют острые ребра. На рис. 4.18 изображен конус с закругленными сторонами и плоским основанием (команда Edit | Cone).

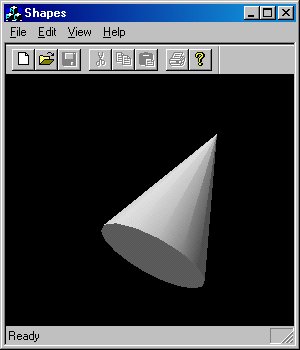
Рис. 4.18. Конус

Если внимательно рассмотреть конус, можно заметить, что его боковая поверхность составлена из 16 треугольников, а основание имеет форму диска. Закраска боковых треугольников создает иллюзию криволинейной поверхности, а закраска основания придает ему плоский вид; между боковой поверхностью и основанием существует резко очерченная граница. Как добиться подобного эффекта?

Стороны конуса строятся точно так же, как и наш первый куб — мы передаем механизму визуализации координаты вершин треугольников, образующих боковую поверхность, и он самостоятельно генерирует нормали, усредняя векторы нормалей для прилегающих граней. Это создает иллюзию кривизны боковой поверхности. Если бы мы просто включили основание конуса в список граней, использованных для создания боковой поверхности, то нормали для основания также были бы определены посредством усреднения нормалей основания и боковых граней. В результате нижняя грань казалась бы выпуклой, а граница между боковой поверхностью и основанием выглядела бы размытой.

Существуют два основных способа для получения плоского основания и резкой границы между основанием и боковой поверхностью. Самое простое, что можно сделать, — это внести основание в список граней с отдельным набором вершин. Разумеется, координаты этих вершин должны совпадать с координатами нижних сторон боковых граней, иначе в фигуре появятся «дырки». Задавая отдельные вершины для нижней грани, мы тем самым указываем, что нижняя грань не имеет прилегающих граней; когда механизм визуализации будет генерировать нормали для вершин основания, он просто использует для этой цели нормаль основания. Такой подход приводит к желаемому результату (плоскому основанию с резким переходом), однако он немного расточителен, поскольку нам приходится задавать лишний набор вершин (в данном случае — 16).

Более разумное решение состоит в том, чтобы использовать для основания конуса те же самые вершины, что и для боковых граней, но при этом задать для них нормали. Именно так работает функция, построившая конус на рис. 4.18. Ее преимущество заключается в том, что нам не придется задавать лишние вершины.

Конечно, хранение нормалей тоже потребует определенных расходов, однако все равно такой подход оказывается более экономичным, поскольку одна и та же нормаль используется для всех вершин основания. Пример программы приведен в следующем разделе, где мы рассматриваем тела вращения (такие, как конус).