| netlib.narod.ru | < Назад | Оглавление | Далее > |
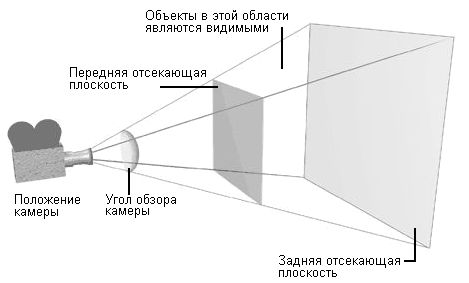
После завершения краткого экскурса в аппаратную область давайте займемся более абстрактными вещами и рассмотрим работу проекционной системы. Поскольку объекты могут находиться в произвольной точке трехмерного пространства, нам нужно как-то определить, что же будет видно в нашем окне. Говоря на языке фотографов, нам необходимо указать направление камеры и фокальное расстояние линз. Кроме того, ради повышения эффективности необходимо задать две отсекающих плоскости: переднюю и заднюю. Все, что находится дальше задней или ближе передней плоскости, не будет воспроизводиться на экране. Усеченная пирамида, изображенная на рис. 2.8, определяет границы видимой области.

Рис. 2.8. Видимая область
Положение передней и задней отсекающих плоскостей задается функциями IRLViewport::SetFront и IRLViewport::SetBack. СОМ-интерфейс IRLViewport применяется для управления портом просмотра. Величину угла камеры можно изменить функцией IRLViewport::SetField. При создании объекта C3dStage некоторым параметрам присваиваются начальные значения, а другие остаются как есть. Если вы посмотрите на реализацию класса C3dStage, то увидите, что в нем отсутствуют специальные функции для изменения параметров видимой области, поскольку стандартные значения хорошо подходят для наших примеров (хотя при желании вы можете самостоятельно написать нужные функции, поэкспериментировать с различными углами камеры и т.д., но пока не стоит опережать события).
Чтобы точно определить положение трехмерного объекта на экране, необходимо применить к его вершинам преобразование, которое отображает трехмерные пространственные координаты на двумерные координаты окна. Преобразование координат осуществляется с помощью матрицы размеров 4 х 4, которая является суперпозицией отдельных преобразований перспективы, масштабирования и переноса. В сущности, для получения двумерных координат вершины следует умножить вектор трехмерных координат на матрицу преобразования. Если вам захочется поближе познакомиться с теорией, я бы порекомендовал книгу «Computer Graphics Principles and Practice» (см. библиографию в конце книги) или какой-нибудь другой учебник по компьютерной графике.
Однако на практике все оказывается несколько сложнее (а разве бывает иначе?). В главе 1 я упоминал о том, что для представления иерархии преобразований в механизме визуализации применяются фреймы. Присоединенные к фреймам объекты могут перемещаться (трансформироваться) по отношению к другим фреймам. Для вычисления двумерных координат любого заданного объекта необходимо совместить результаты преобразований всех фреймов, расположенных в иерархии выше данного объекта, и таким образом определить окончательное преобразование объекта.
| ПРИМЕЧАНИЕ |
Ради наглядности я позволил себе небольшую поэтическую вольность. Фрейм не следует считать физическим объектом вроде изображенного на рис. 2.9; это всего лишь преобразование, применяемое ко всем его потомкам. Соответственно, фрейм не имеет физических размеров или формы. Однако я нередко представляю себе фреймы в виде структур из трубок или соломинок, склеенных друг с другом. Это помогает мне представить взаимное перемещение фреймов, присоединенных к макету. |
Возникает впечатление, что для последовательного выполнения всех этих преобразований потребуется много времени и усилий — и это действительно так, если выполнять все ненужные преобразования. Однако механизм визуализации действует более разумно. Он сохраняет копию матрицы итогового преобразования каждого фрейма (полученную умножением матриц всех преобразований фрейма), и в том случае, если все фреймы, находящиеся в иерархии выше данного, остались без изменений, итоговое преобразование можно не пересчитывать. Следовательно, работа с фреймами не обязательно приводит к потере производительности. На практике, если в вашем макете присутствует несколько движущихся объектов, все равно придется как-то определять их положение. Использование иерархических фреймов для задания относительного положения этих объектов значительно повышает вероятность того, что вам не придется выполнять лишних вычислений. Мы подробнее рассмотрим преобразования в главе 5, так что если вы чувствуете себя слегка сбитым с толку, не теряйтесь — позднее я все объясню.
Объект C3dStage является корнем иерархического дерева фреймов в проекционной системе нашего приложения. Все остальные фреймы так или иначе являются потомками, присоединенными к фрейму сцены. Фрейм камеры и фрейм текущего макета присоединяются непосредственно к фрейму сцены. Все фреймы, входящие в макет, являются потомками фрейма макета. Используя фреймы подобным образом, вы очень легко определяете положение камеры по отношению к макету. Кроме того, можно без труда перемещать камеру по макету, создавая иллюзию полета, или закрепить камеру на одном месте и перемещать весь макет (еще один способ изобразить полет).
При создании фрейма сцены камера находится перед сценой и направляется на ее центр. Другими словами, камера располагается в отрицательной области оси Z. На рис. 2.9 показано взаимное расположение фреймов камеры и сцены.
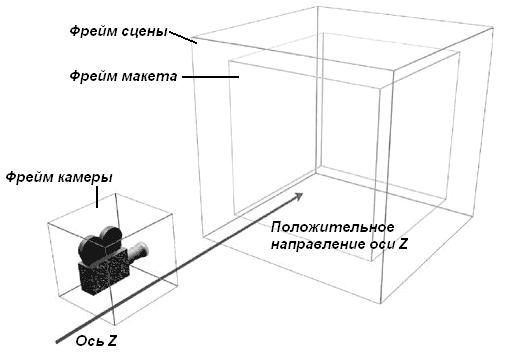
Рис. 2.9. Фрейм камеры и фрейм сцены
Мы еще вернемся к фреймам и их влиянию на положение объекта, когда будем подробнее рассматривать преобразования. А пока давайте рассмотрим, как происходит загрузка фигур из файлов.
| netlib.narod.ru | < Назад | Оглавление | Далее > |