
| netlib.narod.ru | < Назад | Оглавление | Далее > |
Если запустить приложение Basic на приличной машине с хорошей видеокартой, выполняющей аппаратную пересылку битовых блоков (бит-блит), на вас наверняка произведет впечатление скорость его работы. Под «приличной» машиной я имею в виду как минимум компьютер 486 от 50 МГц и выше, а лучше — более современный Pentium с PCI-видеокартой. Именно видеокарта оказывается наиболее важным элементом. Если ваша видеокарта обладает «лишней» видеопамятью (то есть объем видеопамяти превышает тот, который необходим для текущего разрешения экрана) и аппаратными средствами для перемещения блоков видеопамяти, то библиотеки DirectX могут извлечь выгоду из такого положения вещей. При этом достигается заметное повышение скорости по сравнению со старыми видеокартами, в которых для перемещения данных в видеопамяти используется системный процессор. В сущности, именно поддержка аппаратных особенностей видеокарт последнего поколения и составляет одну из самых сильных сторон интерфейса Direct3D — благодаря этому вы добиваетесь от своего компьютера максимальной производительности.
Однако вернемся к нашему примеру. Каждая сфера состоит из 256 граней, которые необходимо нарисовать на экране. Для каждой грани требуется вычислить положение трех или четырех точек. Цвет грани должен изменяться в зависимости от ее положения и суммарного воздействия всех источников света, входящих в макет. Все это сопряжено с немалым объемом вычислений, и плавное движение, которое вы видите на экране, обусловлено тем, что эти вычисления происходят с достаточной скоростью. Библиотека Direct3D — впечатляющий набор программных модулей, оптимизированных с расчетом на максимальную производительность.
| ЗАМЕЧАНИЕ |
Все трехмерные объекты, с которыми нам придется иметь дело, составлены из плоских многоугольников — чаще всего из треугольников. Эти многоугольники являются гранями объекта. А почему они должны быть непременно плоскими? Только для того, чтобы компьютеру было проще и быстрее рисовать их. Некоторые механизмы визуализации могут работать и с криволинейными гранями, однако используемая нами система не входит в их число. Мы научимся создавать объекты в главе 4. |
Что ж, прекрасно — мы похвалили нашу библиотеку, но вы еще не уловили, к чему я клоню? Разумеется, для такого потрясающего быстродействия пришлось кое-чем пожертвовать. Например, на картинке нет ни теней, ни отражений. Возможно, вы даже не обратили на это внимания? Снова запустите программу-пример и понаблюдайте за вращением сфер. Взгляните, откуда падает свет — красная и синяя сфера проходят между белой сферой и направленным источником света, однако на белой сфере не появляются тени. Кроме того, вы не увидите на большой сфере отражений малых сфер.
Механизм визуализации Direct3D не осуществляет трассировки лучей, поэтому он не умеет генерировать теней и отражений. Как следствие, мы получаем значительное увеличение быстродействия. Если вы не заметили отсутствия теней до того момента, когда я вам об этом сказал, то согласитесь с тем, что впечатляющие трехмерные анимации могут обходиться и без теней с отражениями. Как мы узнаем позднее, на самом деле можно генерировать тени и даже имитировать отражения при помощи методики, которая называется хромовым покрытием (chrome wrap), рассмотренной в главе 8, — так что не огорчайтесь и продолжайте читать дальше.
Как видно из текста программы, для вращения большой белой сферы в нашем макете применен вызов функции SetRotation. При запуске приложения можно убедиться, что белая сфера вращается — затенение выполнено настолько качественно, что это даже не сразу видно. Тем не менее можно сразу же заметить, что две меньшие сферы вращаются вокруг большей. Но где же программный код, вызвавший их вращение? Секрет заключается в том, как они были присоединены к макету. Обратите внимание на то, что большая сфера присоединялась непосредственно к макету:
scene.AddChild(&sh1);
тогда как меньшие сферы присоединялись к большой сфере:
sh1.AddChild(&sh2);
sh1.AddChild(&sh3);
Благодаря этому меньшие сферы начинают вращаться вместе с ней. Возможность иерархического закрепления объектов часто встречается в системах трехмерного синтеза изображений.
Для каждого объекта в создаваемом нами макете существует связанный с ним фрейм. Фрейм представляет собой описание математического преобразования (положения, размера или характера объекта), которое должно быть применено ко всем объектам и фреймам, присоединенным к данному фрейму, перед их обсчетом. К фрейму могут присоединяться и другие фреймы-потомки; соответствующие им преобразования выполняются после родительских. В результате фреймы-потомки перемещаются вместе с родительским фреймом и также могут обладать самостоятельным движением по отношению к родителю. Чтобы лучше понять это, представьте, что вы расхаживаете по офису внутри большого здания. Ваш фрейм — это офис, в котором вы находитесь. Родительским фреймом офиса может быть целый этаж, а родительским фреймом этажа — все здание, в котором вы находитесь. Хотя вы замечаете только свое движение по офису, вы также перемещаетесь относительно этажа и всего здания. Эта тема будет подробно рассмотрена в главе 5, где мы займемся преобразованиями, и в главе 6, где показано, как происходит движение объектов.
При реализации библиотеки объектов 3dPlus я решил закрепить за каждым макетом отдельный фрейм. Каждая фигура и источник света также обладают собственным фреймом. Таким образом, вы можете взять произвольный набор объектов и присоединить их к общему фрейму или друг к другу так, как сочтете нужным.
Для чего же все это нужно? Существует множество эффектов, которые чрезвычайно просто реализуются при помощи иерархии объектов/фреймов. Давайте рассмотрим космический тяжелый танк Mark VII, в котором, как известно, для наведения пушек используется допплеровский радар, работающий в Х-диапазоне. Если бы нам понадобилось смоделировать этот танк в нашем трехмерном приложении, мы бы создали геометрическое тело, изображающее радар, присоединили его к башне танка и заставили вращаться вокруг своей оси. Если описывать ситуацию в терминах фреймов, то фрейм радара становится потомком по отношению к фрейму башни. После этого можно сосредоточиться на перемещении танка и забыть про радар — он всегда будет находиться в правильном положении и вращаться. На рис. 1.3 изображен танк Mark VII в действии.

Рис. 1.3. Космический тяжелый танк Mark VII с допплеровским радаром
Последнее, о чем мне хотелось бы упомянуть в этой главе, — это система координат. Поскольку мы работаем с тремя измерениями, положение каждой точки представляется тремя координатами. У нас имеются три оси — X, Y и Z, организованные в так называемую левостороннюю систему координат. Давайте проведем небольшой эксперимент (если вы читаете эту книгу, лежа в кровати, то предупредите свою лучшую половину о том, что вы сейчас начнете делать странные жесты руками — иначе происходящее может быть воспринято как намек). Вытяните левую руку перед собой и выпрямите пальцы; ладонь обращена вправо, а большой палец находится сверху. Поднимите большой палец, затем подогните мизинец и безымянный палец к ладони и отведите средний палец вправо. Ваша рука должна выглядеть примерно так, как показано на рис. 1.4; большой палец изображает ось Y, указательный — ось Z, а средний — ось X.
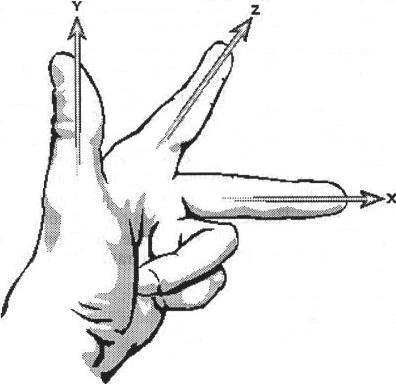
Рис. 1.4. Левая рука с левосторонней системой координат
В левосторонней системе координат ось Y направлена вверх, ось X — вправо, а ось Z — в глубь экрана (от пользователя). Разумеется, название обусловлено вовсе не тем, что вы можете превратить свою левую кисть в какую-то странную фигуру. Если взять винт с левой нарезкой и вращать его от оси X к оси Y, он начнет двигаться по направлению оси Z. Для того чтобы это правило работало в левосторонней системе координат, понадобится винт именно с левой нарезкой.
Многие трехмерные программы основаны на правосторонней системе координат, однако к нашему случаю это не относится, так что привыкайте смотреть на свою левую руку в тех случаях, когда вам нужно сообразить, какая ось куда направлена. Если вы всей душой ненавидите левостороннюю систему координат и страстно желаете перейти к правосторонней, это не так уж сложно. Стоит добавить простейшее преобразование к правосторонней системе координат, и она превратится в левостороннюю, используемую механизмом визуализации. Такие преобразования рассматриваются в главе 5.
Координаты точки в трехмерном пространстве могут передаваться в программные модули DirectX одним из двух способов. Иногда координаты передаются в виде тройки значений типа double, соответствующих координатам X, Y и Z, а иногда — в виде структуры D3DVECTOR, членами которой являются те же самые координаты. В любом случае координаты представляются значениями с плавающей точкой. Выбор масштаба оставляется исключительно на усмотрение пользователя, но я решил установить камеру и другие параметры сцены так, чтобы единичный куб, помещенный в точку 0,0,0 сцены, имел нормальные размеры. Позднее мы снова вернемся к координатам и всему, что с ними связано.
| ЗАМЕЧАНИЕ |
Библиотека 3dPlus содержит класс C3dVector, являющийся производным от класса D3DVECTOR. Всюду, где в качестве аргумента функции выступает тип D3DVECTOR, вместо него можно использовать объект C3dVector. Я создал класс C3dVector, поскольку класс C++ в программе приносит больше пользы, чем простая структура. Кроме того, вы можете обратить внимание на то, что функции Direct3D получают аргументы типа float, а не double. Я использовал значения типа double в своем коде, потому что они дают большую точность, легче преобразуются и используются во всех математических runtime-библиотеках С. |
| netlib.narod.ru | < Назад | Оглавление | Далее > |