
| netlib.narod.ru | < Назад | Оглавление | Далее > |
Тела вращения я впервые увидел в раннем детстве. Мой отец работал токарем, стоял целый день у токарного станка и точил фланцы, стержни, винты с нарезкой, трубы и т.д. (рис. 4.19). Токарный станок вращает металлическую заготовку, зажатую в патроне. К заготовке подносится резец, который срезает ненужный материал при вращении заготовки; положение резца определяет радиус детали. Продольное перемещение резца с одновременным вращением заготовки позволяет выточить стержень (гладкий или нарезной). Основная идея моего рассказа заключается в том, что твердый объект можно описать с помощью простой функции, определяющей радиус объекта в любой точке его длины.

Рис. 4.19. Токарный станок
Процесс построения тел вращения мало чем отличается от создания других трехмерных объектов. Необходимо задать набор вершин, определить, к каким граням они относятся, и затем при желании указать нормали. Поскольку тело вращения можно описать функцией зависимости радиуса от продольной координаты, нетрудно создать фрагмент программы, в котором такая функция используется для генерации вершин и данных граней. На рис. 4.20 изображено тело вращения, построенное именно этим способом. Чтобы увидеть тело вращения на экране, выполните команду Edit | Solid of Revolution.
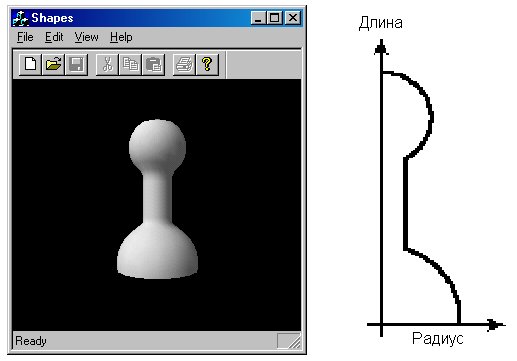
Рис. 4.20. Тело вращения
Ниже приводится фрагмент приложения Shapes, в котором создается изображенный на рисунке объект:
double RevolveFn(double z, void* pArg)
{
if (z < -1.1) {
return sqrt(1 — (z + 2)*(z + 2));
} else if (z > 0.8) {
return sqrt(2 — (z — 2)*(z — 2));
} else {
return 0.5;
}
}
// Создать тело вращения
void CMainFrame::OnEditSolidr()
{
// Создать объект по заданной функции
NewScene();
m_pShape = new C3dShape;
m_pShape->CreateRSolid(-3.0, 2.2, 0.2, TRUE, TRUE,
RevolveFn, NULL, 16);
m_pScene->AddChild(m_pShape);
// Развернуть объект, чтобы показать его со стороны
m_pShape->SetDirection(0, -1, 0);
}
Как видите, в данном случае мы имеем дело с двумя функциями. RevolveFn возвращает значения радиуса для заданной продольной координаты, а функция OnEditSolidr вызывается при выполнении команды меню Edit | Solid of Revolution. Для построения объекта внутри функции OnEditSolidr вызываются функции RevolveFn и C3dShape::CreateRSolid. Аргументы CreateRSolid выглядят несколько необычно, поэтому позвольте мне объяснить их назначение.
Создавая функцию CreateRSolid, я не собирался делать ее универсальной. Вместо того чтобы обрабатывать координаты концов объекта, я решил всегда строить фигуру вдоль оси Z. Таким образом, написанная вами функция (в данном случае RevolveFn) возвращает радиус объекта как функцию координаты по оси Z. Аргументами CreateRSolid являются максимальное и минимальное значения координат по оси Z, приращение по оси Z, две логические величины, определяющие необходимость замыкания концов фигуры, указатель на функцию радиуса, необязательный аргумент, передаваемый в функцию радиуса, и наконец количество граней в круговой поверхности.
В нашем случае необязательный аргумент функции радиуса не используется, однако вы, например, можете передать в нем указатель на какую-нибудь таблицу данных. При таком подходе можно написать обобщенную функцию, которая строила бы более сложные тела вращения с использованием данных таблицы.
После того как объект будет создан, вам наверняка захочется развернуть его и переместить в итоговое положение. Как видно на примере функции OnEditSolidr в приведенном выше фрагменте, я развернул объект так, чтобы он был обращен вдоль оси Y, а не вдоль своей первоначальной оси Z.
Давайте посмотрим, как работает функция C3dShape::CreateRSolid. Приведенный ниже фрагмент взят из библиотеки 3dPlus:
// Создание тел вращения
BOOL C3dShape::CreateRSolid(double z1, double z2, double dz,
BOOL bClosed1, BOOL bClosed2,
SOLIDRFN pfnRad, void* pArg,
int nFacets)
{
New();
ASSERT(pfnRad);
ASSERT(dz != 0);
int iZSteps = (int)((z2 — z1) / dz);
if (iZSteps < 1) return FALSE;
int iRSteps = nFacets;
if (iRSteps < 8) iRSteps = 8;
double da = _twopi / iRSteps;
// Создать массив для вершин
int iVertices = (iZSteps + 1) * iRSteps;
D3DVECTOR* Vertices = new D3DVECTOR [iVertices];
D3DVECTOR* pv = Vertices;
// Создать массив для данных граней.
// Каждая грань имеет 4 вершины, за исключением торцов.
int iFaces = iZSteps * iRSteps;
int iFaceEntries = iFaces * 5 + 1;
if (bClosed1) iFaceEntries += iRSteps + 1;
if (bClosed2) iFaceEntries += iRSteps + 1;
int* FaceData = new int [iFaceEntries];
int* pfd = FaceData;
// Заполнить координаты вершин
double z = z1;
double r, a;
for (int iZ = 0; iZ <= iZSteps; iZ++) {
r = pfnRad(z, pArg);
a = 0;
for (int iR = 0; iR < iRSteps; iR++) {
pv->x = D3DVAL(r * sin(a));
pv->y = D3DVAL(r * cos(a));
pv->z = D3DVAL(z);
pv++;
a += da;
}
z += dz;
}
// Заполнить список граней
int iFirst = iRSteps;
for (iZ = 0; iZ < iZSteps; iZ++) {
for (int iR = 0; iR < iRSteps; iR++) {
*pfd++ = 4; // Количество вершин в грани
*pfd++ = iFirst + iR;
*pfd++ = iFirst + ((iR + 1) % iRSteps);
*pfd++ = iFirst — iRSteps +
((iR + 1) % iRSteps);
*pfd++ = iFirst — iRSteps + iR;
}
iFirst += iRSteps;
}
*pfd = 0; // Завершить список
// Создать круговую поверхность с автоматической
// генерацией нормалей
BOOL b = Create(Vertices, iVertices, NULL, 0,
FaceData, TRUE);
delete [] FaceData;
FaceData = new int [iRSteps * 2 + 2];
D3DVECTOR nvect [] = {
{0, 0, 1},
{0, 0, -1}
};
if (bClosed1) {
pfd = FaceData;
*pfd++ = iRSteps;
for (int iR = 0; iR < iRSteps; iR++) {
*pfd++ = iR;
*pfd++ = 1;
}
*pfd = 0;
m_hr = m_pIMeshBld->AddFaces(iVertices, Vertices,
2, nvect,
(ULONG*)FaceData,
NULL);
ASSERT(SUCCEEDED(m_hr));
}
if (bClosed2) {
pfd = FaceData;
*pfd++ = iRSteps;
iFirst = iRSteps * iZSteps;
for (int iR = 0; iR < iRSteps; iR++) {
*pfd++ = iRSteps — 1 — iR + iFirst;
*pfd++ = 0;
}
*pfd = 0;
m_hr = m_pIMeshBld->AddFaces(iVertices, Vertices,
2, nvect,
(ULONG*)FaceData,
NULL);
ASSERT(SUCCEEDED(m_hr));
}
delete [] Vertices;
delete [] FaceData;
m_strName = "Solid of revolution";
return b;
}
На первом этапе, после выполнения инициализации, по функции радиуса заполняется список вершин. Затем генерируются данные боковых граней и создается исходная форма. Если при вызове функции были заданы замкнутые концы фигуры, создается новый набор данных для граней-торцов, однако на этот раз с нормалями, управляющими процессом закраски, чтобы торцы фигуры казались плоскими. Новые грани добавляются к существующей фигуре.
Возможно, вы обратили внимание на то, что фигуре присваивается имя (в данном случае — Solid of Revolution, хранящееся в переменной m_strName). Когда мы будем заниматься выбором объектов в макете, имя сообщит пользователю, какая фигура выбрана им в настоящий момент.
Мы очень кратко пробежались по большому фрагменту программы, и у вас наверняка осталось много вопросов по поводу его работы и назначению отдельных функций. Если вы хотите понять, как устроена функция CreateRSolid, возьмите лист бумаги в клетку, сверните его в трубку и затем представьте себе, что вам потребовалось описать каждое продольное ребро и каждую грань этой решетки. Именно это и происходит в приведенном выше фрагменте, а эксперимент с трубкой описывает мой подход к его написанию. Во фрагменте присутствуют несколько вызовов функций интерфейсов Direct3D, назначение которых можно узнать в документации по DirectX 2 SDK. Заодно найдите в SDK макрос D3DVAL и посмотрите, что он делает.
В главе 5 мы научимся преобразовывать фигуры, применяя к ним операции вращения, переноса и масштабирования. После прочтения этой главы можете модифицировать функцию CreateRSolid так, чтобы при ее вызове можно было бы задать координаты конечных точек фигуры — функция станет более полезной.
| netlib.narod.ru | < Назад | Оглавление | Далее > |