Преобразования трехмерных объектов

Теперь давайте посмотрим, как матричные преобразования используются на практике, при работе с трехмерными объектами. Чтобы применить матрицу преобразования к объекту C3dShape, вовсе не нужно заниматься умножением. Вместо этого следует скомбинировать новое преобразование с текущим, хранящимся во фрейме объекта. Вспомните — фрейм, определяющий положение и ориентацию объекта в макете, на самом деле представляет собой преобразование, применяемое ко всем точкам фигуры. Кроме того, фрейм объекта является потомком другого фрейма, расположенного выше в иерархии, и для определения окончательного положения объекта необходимо скомбинировать результаты всех преобразований в иерархии фреймов. Мы собираемся изменить преобразование, хранящееся во фрейме объекта, расположенном где-то внизу иерархии фреймов, пример которой изображен на рис. 5.1.

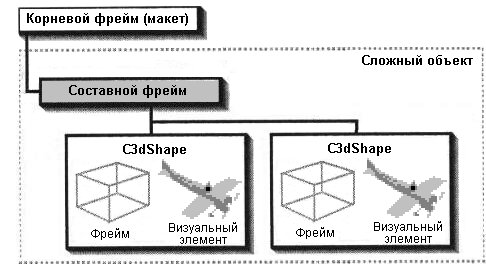
Рис. 5.1. Иерархия фреймов

Изображенный на рис. 5.1 сложный объект состоит из двух фигур, каждая из которых обладает собственным фреймом и визуальным элементом. Для преобразования всего объекта следует модифицировать объединяющий фрейм, который является общим родителем для фреймов обоих компонентов.

Преобразование фрейма можно изменить тремя способами, а именно включив новое преобразование перед текущим, после него или же заменить им текущее преобразование. Как определить, какой из способов следует использовать в каждом конкретном случае? Я надеюсь, что после знакомства с примерами вы и сами найдете ответ на этот вопрос.

Все преобразования, которые мы будем рассматривать, содержатся в приложении TransFrm. Для демонстрации я выбрал самолет, поскольку его положение в макете и ориентация определяются с первого взгляда. На рис. 5.2 изображено начальное состояние самолета, находящегося в начале координат.

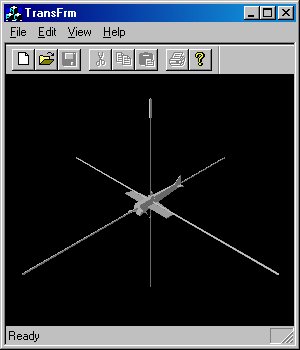
Рис. 5.2. Окно приложения до применения преобразований

Перенос

Первый тип рассматриваемых нами преобразований — перенос. Переносом называется простое прямолинейное перемещение объекта в одном направлении. Для переноса объекта следует прибавить к его координатам x, y и z величины смещений. На рис. 5.3 изображен результат переноса по оси X.

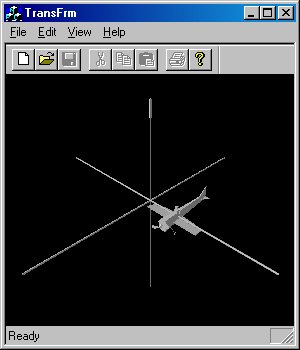
Рис. 5.3. Перенос по оси X

Фрагмент программы, в котором был осуществлен этот перенос, выглядит следующим образом:

void CMainFrame::OnEditTranslatex()
{
    if (!m_pCurShape) return;
    C3dMatrix m;
    m.Translate(2, 0, 0);
    m_pCurShape->AddTransform(m, D3DRMCOMBINE_AFTER);
} 

Сначала мы создаем объект C3dMatrix для хранения матрицы переноса (в данном случае, для смещения на 2 единицы вдоль оси X). Затем преобразование применяется к текущей фигуре. Обратите внимание на аргумент D3DRMCOMBINE_AFTER, который указывает на необходимость применения преобразования после любых существующих преобразований. Другими словами, после завершения всех преобразований появляется дополнительный перенос объекта вдоль оси X.

Поворот

Теперь давайте развернем наш самолет, расположенный в начале координат, на 45 градусов вокруг оси Y. Результат изображен на рис. 5.4.

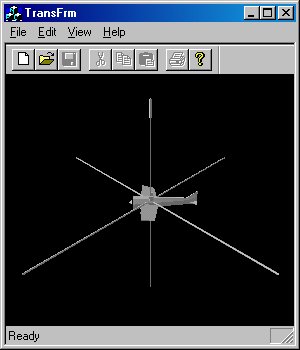
Рис. 5.4. Поворот вокруг оси Y

Ниже приведен текст функции, в которой выполняется поворот:

void CMainFrame::OnEditRotatey()
{
    if (!m_pCurShape) return;
    C3dMatrix m;
    m.Rotate(0, 45, 0);
    m_pCurShape->AddTransform(m, D3DRMCOMBINE_AFTER);
} 

Масштабирование

Еще один тип преобразований объекта — масштабирование, увеличивающее или уменьшающее его размеры. Самое интересное заключается в том, что для каждой оси можно выбрать свой коэффициент масштабирования. На рис. 5.5 показано, как будет выглядеть самолет после растяжения только по осям X и Y.

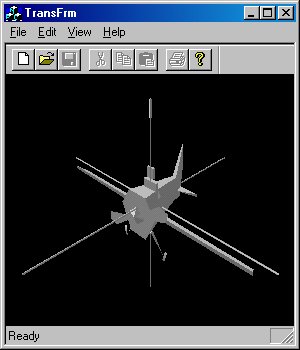
Рис. 5.5. Масштабирование объекта по осям X и Y

Наш самолет выглядит по меньшей мере странно! Результат последующего применения аналогичного масштабирования по оси Z изображен на рис. 5.6.

Рис. 5.6. Объект после равномерного масштабирования по осям X, Y и Z

Масштабирование в программе мало чем отличается от других, рассмотренных выше преобразований. Ниже приведен пример того, как выполняется масштабирование только по оси X:

void CMainFrame::OnEditScalex()
{
    if (!m_pCurShape) return;
    C3dMatrix m;
    m.Scale(2.0, 1.0, 1.0);
    m_pCurShape->AddTransform(m, D3DRMCOMBINE_AFTER);
} 

Обратите внимание на то, что коэффициенты масштабирования по осям Y и Z равны 1, а не 0. Если присвоить им нулевые значения, вам будет нелегко рассмотреть свой объект!

Порядок преобразований

Мы рассмотрели отдельные преобразования переноса, поворота и масштабирования. Теперь давайте посмотрим, что происходит при выполнении серии последовательных преобразований. Начнем с переноса вдоль оси X, за которым следует поворот вокруг оси Y. Результат изображен на рис. 5.7.

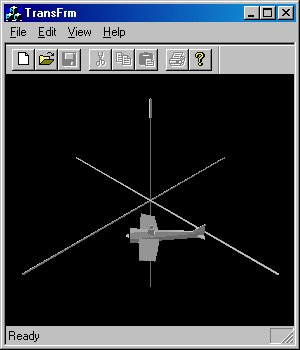
Рис. 5.7. Перенос вдоль оси X, за которым следует поворот вокруг оси Y

Совпадает ли такой результат с тем, что вы ожидали увидеть? Текст функции приведен ниже:

void CMainFrame::OnEditTranrot()
{
    if (!m_pCurShape) return;
    C3dMatrix m;
    m.Translate(3, 0, 0);
    m.Rotate(0, 45, 0);
    m_pCurShape->AddTransform(m, D3DRMCOMBINE_AFTER);
} 

Как видите, мы осуществили перенос на 3 единицы вдоль оси X, после чего развернули объект на 45 градусов вокруг оси Y. Во время поворота самолет находился на расстоянии в 3 единицы от начала координат. Следовательно, самолет описал дугу в 45 градусов по окружности радиусом в 3 единицы.

Давайте повторим те же самые преобразования, но на этот раз изменим их порядок. Результат изображен на рис. 5.8.

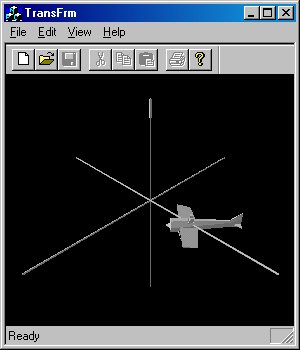
Рис. 5.8. Поворот вокруг оси Y, за которым следует перенос вдоль оси X

Как видите, результат значительно отличается от предыдущего. На этот раз все выглядит так, словно после переноса самолет развернулся вокруг собственной оси, а не вокруг оси Y макета.

Только что мы сделали важное открытие: порядок применения преобразований чрезвычайно важен. Кроме того, мы выяснили, что для того, чтобы повернуть объект вокруг оси макета, следует применять поворот после всех переносов; для того, чтобы объект вращался вокруг его собственной оси, поворот следует применить до переносов. Это необходимо знать, если вы хотите в полной мере контролировать положение всех объектов. В главе 6 мы воспользуемся этой методикой для имитации полета.

В нашем приложении имеются команды меню, поворачивающие объект вокруг осей макета, по аналогии с первым фрагментом кода данного раздела. Сюда также включены команды для выполнения поворотов вокруг собственной оси объекта. Ниже приводится пример поворота вокруг оси Y объекта:

void CMainFrame::OnEditRobjy()
{
    if (!m_pCurShape) return;
    C3dMatrix m;
    m.Rotate(0, 45, 0);
    m_pCurShape->AddTransform(m, D3DRMCOMBINE_BEFORE);
} 

С первого взгляда кажется, что данный фрагмент полностью совпадает с приведенным в разделе «Поворот», но более внимательное рассмотрение показывает, что поворот на этот раз выполняется до текущего преобразования (D3DRMCOMBINE_BEFORE), а не после него.

Возвращение на базу

Полет подходит к концу, и настало время возвращаться обратно. Наше приложение содержит команду Edit | Reset, которая возвращает объект в начало координат и возвращает ему исходное положение и ориентацию. Ниже приведена соответствующая функция:

void CMainFrame::OnEditReset()
{
    if (!m_pCurShape) return;
    C3dMatrix m;
    m_pCurShape->AddTransform(m, D3DRMCOMBINE_REPLACE);
} 

Вам может показаться, что здесь допущена какая-то ошибка — ведь для матрицы вообще не задано никакого преобразования. Однако на самом деле именно это нам и нужно! Обратите внимание на использование аргумента D3DRMCOMBINE_REPLACE, заменяющего любое текущее преобразование новой матрицей. Конструктор матрицы инициализирует ее элементами единичной матрицы; заменяя текущую матрицу фрейма на матрицу идентичного преобразования, мы возвращаем объект в исходное состояние.

Экспериментируйте!

В приложении имеется окно диалога, открываемое командой Edit | Transform Shape. Оно используется для задания произвольных преобразований переноса, поворота и масштабирования. В любом случае можно указать, следует ли применять новое преобразование до текущего, после него или же заменить текущее преобразование новым. Несколько опытов с окном диалога Transforms, изображенным на рис. 5.9, заполнят все возможные пробелы в вашем понимании того, как же комбинируются преобразования.

Рис. 5.9. Окно диалога Transforms

Житейские мелочи

На самом деле мы рассмотрели не все преобразования, которые могут быть применены к фигуре, а ограничились лишь самыми полезными из них. Я хотел бы закончить эту главу небольшим лирическим отступлением и продемонстрировать вам еще одно, последнее преобразование. Сдвигом называется преобразование, которое перекашивает объект в боковом направлении. Например, положите на стол колоду аккуратно сложенных карт и толкните ее верх в сторону, чтобы края колоды по-прежнему оставались прямыми, но не были перпендикулярны столу, как показано на рис. 5.10.

Рис. 5.10. «Сдвинутая» колода карт

Итак, мы применили к колоде преобразование сдвига. На рис. 5.11 показано, что получится в результате применения сдвига к нашему самолету.

Рис. 5.11. Результат применения сдвига

Чтобы вам было легче разглядеть самолет после сдвига, я немного увеличил его, применив перед сдвигом масштабирование с одинаковыми коэффициентами по всем трем осям. Я не смог придумать для сдвига достойного применения в трехмерном приложении, но наверняка вы сможете это сделать, поэтому я привожу текст функции, выполнившей преобразование сдвига на рис. 5.11:

void CMainFrame::OnEditShear()
{
    if (!m_pCurShape) return;
    C3dMatrix m;
    m.m_12 = 2;
    m_pCurShape->AddTransform(m, D3DRMCOMBINE_BEFORE);
} 

Как нетрудно убедиться из листинга, в классе C3dMatrix нет специальной функции сдвига, поэтому я задал матрицу вручную, указав значение одного из элементов. В данном случае сдвиг выполняется вдоль оси Z. Разумеется, вы можете сдвигать объекты и по другим осям. Вопрос о том, какие значения должны иметь элементы матрицы для этих сдвигов, оставляю для самостоятельного изучения (возможно, после того, как ответ на него будет найден, вы сможете включить в класс C3dMatrix отсутствующую функцию сдвига).