
| netlib.narod.ru | < Назад | Оглавление | Далее > |
Иногда требуется создать поверхность, которая имитирует пересеченный рельеф местности, холмы или что-нибудь другое, подсказанное вашей фантазией. Приложение Shapes демонстрирует два различных алгоритма для построения случайных рельефов. В первом случае используется решетка из точек, высота которых выбирается случайным образом. Во втором алгоритме грань, в центре которой определяется точка со случайной высотой, делится на несколько вспомогательных граней. Деление повторяется до тех пор, пока количество граней не станет достаточно большим, а ландшафт будет выглядеть достаточно интересно.
Давайте сначала рассмотрим алгоритм с решеткой. На рис. 4.21 изображен пример ландшафта, построенного по решетке из точек со случайной высотой (команда Edit | Landscape 1).

Рис. 4.21. Случайный ландшафт, построенный с помощью решетки
Функция для построения поверхности, образующей ландшафт, напоминает функцию для создания тел вращения. В данном случае мы передаем функцию, которая генерирует высоту точки по значениям X и Z. Ниже приведен фрагмент приложения Shapes:
double LandscapeFn(double x, double z, void* pArg)
{
return -2.0 + (double)(rand() % 100) / 100;
}
// Создать поверхность, изображающую ландшафт
void CMainFrame::OnEditInsland()
{
// Создать поверхность с использованием функции высоты
NewScene();
m_pShape = new C3dShape;
m_pShape->CreateSurface(-5, 5, 1, -10, 10, 1,
LandscapeFn, NULL);
m_pScene->AddChild(m_pShape);
}
Высота опорных точек определяется случайным образом, а ландшафт создается функцией C3dShape::CreateSurface. Данная функция похожа на C3dShape::CreateRSolid, так что я не стану понапрасну утомлять вас подробностями.
| ПРИМЕЧАНИЕ |
Ландшафт, который вы видите на своем экране, может отличаться от изображенного на рис. 4.21. Иногда в изображении вдруг появляются странные пики; это явление обусловлено ошибкой в текущей версии DirectX. Более подробная информация, включающая возможные пути борьбы с пиками, приводится в файле Readme.txt на прилагаемом диске CD-ROM. А пока можно попробовать изменить размер окна, чтобы пик исчез из него. |
От смехотворно простого алгоритма перейдем к более серьезному и посмотрим, как строится поверхность в алгоритме деления граней. На рис. 4.22 изображен ландшафт, построенный по новому алгоритму (команда Edit | Landscape 2).
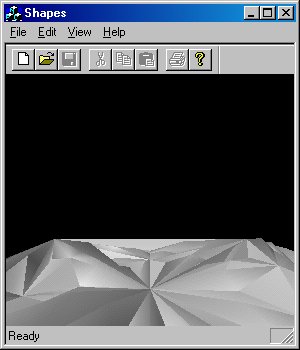
Рис. 4.22. Ландшафт, построенный по алгоритму деления граней
Все грани на рис. 4.22 выглядят плоскими и имеют острые края, потому что создавшая их функция пользуется отдельным набором вершин для каждой новой грани. Как мы убедились раньше, в разделе «Создание простых фигур», для той грани, у которой отсутствуют прилегающие грани, по умолчанию создаются нормали вершин, направления которых совпадают с нормалью к грани. Получившаяся грань выглядит плоской. При желании можно модифицировать программу так, чтобы она генерировала нормали вместе с вершинами, или же немного усложнить код и создавать грани с общими вершинами. Давайте сначала рассмотрим алгоритм, по которому создавалась поверхность на рис. 4.22, а затем — исходный текст программы.
Внутри каждой грани поверхности выбирается точка. Я решил определять положение этой точки, усредняя координаты всех вершин грани. Выбрав точку,которой суждено превратиться в отдельную вершину, мы генерируем случайную высоту для новой вершины и создаем новый набор граней. На рис. 4.23 показана прямоугольная грань, разделенная в соответствии с алгоритмом.
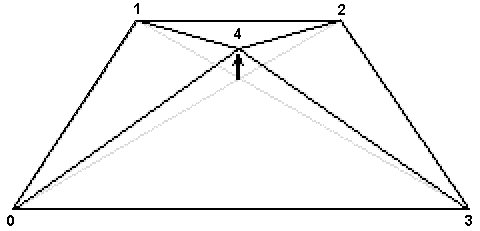
Рис. 4.23. Грань, разделенная на четыре новые грани
После того как будут созданы четыре новые грани, процесс повторяется — четыре новые треугольные грани делятся на новые треугольники, как показано на рис. 4.24.

Рис. 4.24. Грани после повторного деления
На рисунке довольно трудно понять пространственное положение всех граней, однако вы наверняка уловили общий принцип. Если немного поработать над алгоритмом, он позволит строить довольно реалистичные горы. Давайте посмотрим, как выглядит функция для построения ландшафтов, подобных изображенному на рис. 4.22:
void CMainFrame::OnEditInsland2()
{
// Создать исходную фигуру, которая является
// простейшей прямоугольной гранью.
double x = 10;
double z1 = -10;
double z2 = 20;
D3DVECTOR vlist [] = {
{-x, -4, z1},
{-x, -4, z2},
{ x, -4, z2},
{ x, -4, z1}
};
int nv = sizeof(vlist) / sizeof(D3DVECTOR);
int flist [] = {4, 0, 1, 2, 3, 0};
NewScene();
m_pShape = new C3dShape;
m_pShape->Create(vlist, nv, flist);
// Делить грани на более мелкие
int iCycles = 5;
double dHeight = 1.0;
while (iCycles--) {
// Получить текущий список граней
int nFaces = m_pShape->GetFaceCount();
IDirect3DRMMeshBuilder* pMB = m_pShape->GetMeshBuilder();
ASSERT(pMB);
IDirect3DRMFaceArray* pIFA = NULL;
HRESULT hr;
hr = pMB->GetFaces(&pIFA);
ASSERT(SUCCEEDED(hr));
// Создать новую фигуру, к которой
// будут добавляться новые грани
C3dShape* pNewShape = new C3dShape;
// Перебрать грани из списка
for (int iFace = 0; iFace < nFaces; iFace++) {
IDirect3DRMFace* pIFace = NULL;
hr = pIFA->GetElement(iFace, &pIFace);
ASSERT(SUCCEEDED(hr));
ASSERT(pIFace);
// Получить количество вершин
DWORD nVert = pIFace->GetVertexCount();
// Разместить буферы
D3DVECTOR* pVert = new D3DVECTOR [nVert];
// Получить данные вершин
hr = pIFace->GetVertices(&nVert,
pVert,
NULL);
ASSERT(SUCCEEDED(hr));
ASSERT(pVert);
ASSERT(nVert > 2);
// Выделить память для новых списков вершин и граней
D3DVECTOR* NewVert = new D3DVECTOR [nVert + 1];
int* NewFaceData = new int [4 * nVert + 1];
// Скопировать старые вершины
// и определить суммы координат
C3dVector vNew(0, 0, 0);
for (DWORD i = 0; i < nVert; i++) {
NewVert[i] = pVert[i];
vNew.x += pVert[i].x;
vNew.y += pVert[i].y;
vNew.z += pVert[i].z;
}
// Вычислить положение новой вершины
// на плоскости грани
vNew.x /= nVert;
vNew.y /= nVert;
vNew.z /= nVert;
// Прибавить случайное отклонение высоты
double dh = dHeight * (1.0 — ((double)(rand() %
100)) / 50.0);
vNew.y += dh;
// Добавить новую вершину
NewVert[nVert] = vNew;
// Создать данные граней
int *pfd = NewFaceData;
for (i = 0; i < nVert; i++) {
*pfd++ = 3;
*pfd++ = i;
*pfd++ = (i+1) % nVert;
*pfd++ = nVert; // Новая вершина
}
*pfd = 0;
// Включить новые грани в фигуру
pNewShape->AddFaces(NewVert, nVert + 1, NULL,
0, NewFaceData);
// Удалить списки вершин и граней
delete [] NewVert;
delete [] NewFaceData;
// Удалить данные вершин
delete [] pVert;
// Освободить грань
pIFace->Release();
}
// Освободить массив граней
pIFA->Release();
pMB->GenerateNormals();
// Примечание: не освобождайте интерфейс
// построения сеток!!!
// Удалить старую фигуру и сделать текущей новую.
delete m_pShape;
m_pShape = pNewShape;
}
// Присоединить итоговую фигуру к макету
m_pScene->AddChild(m_pShape);
}
Как я уже говорил, такой подход оказывается несколько более трудоемким, чем простая генерация решетки со случайными значениями высоты. Я не стану подробно объяснять весь приведенный фрагмент, а предлагаю читателю разобраться с ним самостоятельно. Здесь присутствуют несколько функций класса C3dShape и прямые обращения к интерфейсам механизма визуализации в тех случаях, когда соответствующий сервис не вошел в класс C3dShape.
| netlib.narod.ru | < Назад | Оглавление | Далее > |