| netlib.narod.ru | < Назад | Оглавление | Далее > |
Вы хотите нарисовать что-нибудь реалистичное на экране, и ваша задача состоит в представлении трехмерного мира на плоском двухмерном экране. В последующих подразделах вы узнаете об основных подходах, используемых в большинстве архитектур визуализации для отображения геометрических объектов на экране. Я начну с основ, а потом перейду к более развернутому взгляду на то, что творится под капотом у современных видеокарт.
Перед тем, как начать разговор о визуализации, следует поговорить о том, как устроена наша вселенная. Вселенная, которую мы хотим нарисовать, состоит из объектов, которые составлены из молекул. Если мы будем рисовать объекты, учитывая все небольшие частицы из которых они состоят, наша картинка будет выглядеть бесподобно, но мы столкнемся с рядом серьезных проблем. Крошечный объект состоит из миллиардов атомов, и для представления их всех нужен невообразимый объем памяти и такая же мощность процессора.
Примерно такой способ визуализации используется в медицинской технике и называется объемным представлением (volumetric rendering). Однако, даже если вы создадите модель объекта в виде трехмерной матрицы 256 × 256 × 256 элементов, это будет очень грубое приближение и тем не менее для представления даже такого простого объекта понадобится около 64 Мбайт памяти (не говоря уже о затратах процессорного времени на визуализацию такого объекта). Очевидно, что рассмотренный способ может работать в некоторых специализированных областях, но не подходит для общецелевой визуализации.
Поскольку объемное представление вызывает множество проблем, нам нужен другой способ. Если учесть, что большинство объектов, которые мы изображаем твердые и непрозрачные, можно получить гораздо более подходящий к данной ситуации способ представления. Что если мы будем представлять объекты как их внешние оболочки?
Этот подход похож на создание фигур из папье-маше. Сперва мы делаем металлический проволочный каркас, представляющий форму моделируемого объекта. После того, как форма задана, вы облепливаете сетку папье-маше и даете фигуре высохнуть. Ну и чтобы закончить создание фигурки вы используете краски... вуаля!
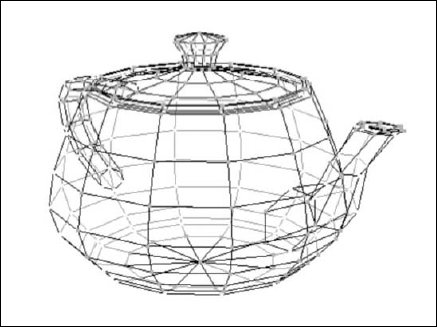
Хотя аналогия выглядит по-детски, это основа подхода, принятого в большинстве современных архитектур трехмерной визуализации. Как видно на рис. 2.1 проволочная сетка аналогична вершинам и граням, которые описывают форму вашего объекта и задают основу для его строительства.

Рис. 2.1. Представление чайника в виде каркаса сетки
Сетка определяет форму, но нам надо сделать объект сплошным. Здесь вступает в действие папье-маше. Как показано на рис. 2.2, точки пересечения линий сетки объединяются в плоские треугольники. Аппаратура визуализации закрашивает эти полигоны и образуется сплошная оболочка вашего объекта.

Рис. 2.2. Представление чайника с помощью полигонов
Возможно, вам будет интересно узнать, почему в большинстве архитектур визуализации в качестве полигонов используются треугольники. Главная причина в том, что треугольник является простейшей фигурой, позволяющей задать область поверхности, и таким образом могущей служить в качестве базового строительного блока для сеток. Хотя вы можете использовать более сложные полигоны, и некоторые архитектуры так делают, при этом появляется две проблемы. Основной проблемой является тот факт, что при использовании в качестве базового примитива более сложных фигур, например квадратов, снижается точность представления сложных поверхностей. Кроме того, математика для растеризации более сложных полигонов (то есть для определения составляющих полигон пикселов) также становится более сложной из-за того, что приходится иметь дело с невыпуклыми полигонами.
Хотя вам и не надо ждать, пока полигоны высохнут, добавить цвета не помешает, и здесь в дело вступают текстуры. Просто примените текстуру (или несколько), освещение и другие способы раскраски, и вы получите реалистично выглядящий твердый объект, как тот, что изображен на рис. 2.3.

Рис. 2.3. Чайник с наложенной текстурой
Конечно, то насколько реалистично будет выглядеть ваш объект, во многом зависит от того, насколько точно составлена сетка и как много текстур вы применили. Это компромисс, которого надо достигнуть, сбалансировав параметры визуализации, основываясь на сфере применения, желаемом реализме и производительности.
Мы рассмотрели случай с одним объектом. Но вселенная состоит из многих объектов. Что, если вам надо отобразить несколько чайников, или, например, чайник и резинового утенка? Каждый объект во вселенной должен быть где-то размещен, и сейчас мы обсудим, как этого достигнуть.
Расположение объекта в мире представляется тремя составляющими: местоположением, поворотом и масштабом. Хотя существует множество различных способов представления этих трех компонент расположения, общепринятым способом является представление в виде матриц.
Для вершин объекта указывается их местоположение относительно центра объекта, такое представление называется пространством объекта (object space). Вы можете представить объект в мире, назначив ему матрицу преобразования, которая будет преобразовывать вершины объекта из пространства объекта в мировое пространство, то есть систему координат, описывающую вселенную.
В следующих подразделах вы узнаете, как каждая из трех составляющих может быть представлена с использованием матриц.
Расположение объекта в пространстве требует, чтобы объекту дали трехмерные пространственные координаты. Координаты отсчитываются от начала мировой системы, местоположение которого выбирается произвольным образом. На рис. 2.4 показано перемещение и представляющая его матрица.
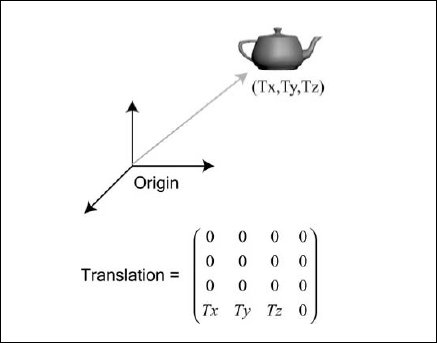
Рис. 2.4. Перемещение и его матричное представление
Иногда объекты надо масштабировать, потому что их размер в мире должен отличаться от размера, в котором они были созданы. Масштабирование может выполняться независимо по каждой из трех осей. Представление масштабирования в матричной форме показано на рис. 2.5.
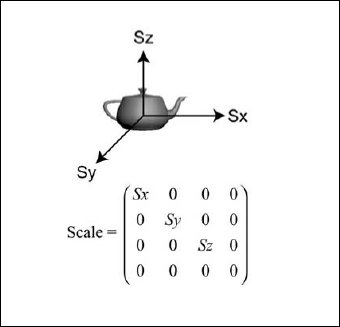
Рис. 2.5. Масштабирование и его матричное представление
Помимо позиционирования и масштабирования объектов в вашем мире, их нужно вращать. В матричной форме вращение представляется последовательностью поворотов относительно осей X, Y и Z объекта. Вращение и его матричное представление показаны на рис. 2.6.
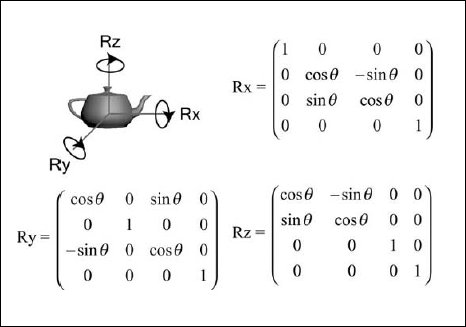
Рис. 2.6. Вращение и его матричное представление
Теперь, когда вы понимаете, как можно представить базовые преобразования в виде матриц, необходимо понять, как комбинировать эти операции для получения итоговой матрицы преобразования, используемой для преобразования представления объекта из пространства объекта в мировое пространство. Комбинирование нескольких преобразований в матричной форме достаточно просто и выполняется путем перемножения матриц между собой. Это все, что я скажу об операциях с матрицами и линейной алгебре, поскольку это необходимый минимум, который вы должны уже знать, чтобы размещать объекты на экране. Если для вас все это похоже на тарабарщину, я настоятельно рекомендую вам обратиться к более полной книге о трехмерной визуализации или к учебнику линейной алгебры, чтобы изучить трехмерную математику. Попробуйте почитать книгу Кристофера Тремблэя «Course's Mathematics for Game Developers».
К этому моменту вы должны понимать, как представить объекты трехмерного мира для целей визуализации. Я также дал краткий обзор того, как расположить эти объекты в вашем виртуальном мире с помощью матричных операций преобразования. Однако этого недостаточно, чтобы вы могли визуализировать ваш мир на экране; кое-чего не хватает. Мы смотрим на виртуальный мир через экран и это очень похоже на съемку видеокамерой в реальном мире. Чтобы воспроизвести такое поведение, нам надо разместить виртуальную камеру в нашем виртуальном мире. Сама по себе камера позиционируется в мире тем же самым образом, что и остальные объекты — с помощью матрицы преобразования. Это показано на рис. 2.7.
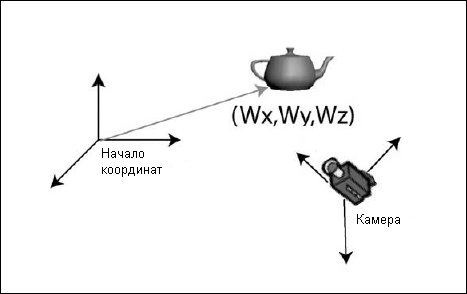
Рис. 2.7. Простая сцена с камерой
После того, как мы разместили в нашем мире камеру, для визуализации нашей сцены необходимо получить представление объектов относительно камеры, или в пространстве камеры. Чтобы сделать это, нам надо применить инвертированную матрицу камеры для преобразования каждого объекта. Вычисление инвертированной матрицы выходит за рамки данной главы, но в его основе лежит применение преобразований, обратных тем которые использовались для размещения камеры.
Получив инвертированную матрицу камеры, мы можем комбинировать ее с матрицей преобразования каждого объекта и получить матрицу преобразования в пространство камеры для каждого объекта. Это комбинированное преобразование, показанное на рис. 2.8, по существу представляет объекты относительно местоположения камеры, а не относительно начала координат мировой системы.
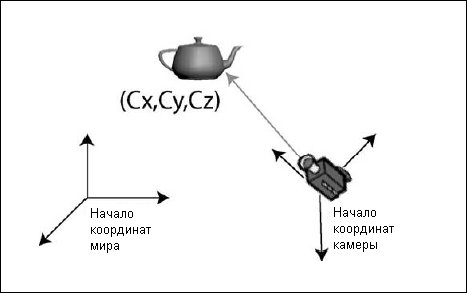
Рис. 2.8. Преобразование объекта из мирового пространства в пространство камеры
Уже можно визуализировать? Не совсем. Наша камера размещена в мире, но нам надо визуализировать на экран. К сожалению, экраны компьютеров пока остаются плоскими и двухмерными, и нам надо представить нашу трехмерную геометрию на плоской двухмерной поверхности. Этот процесс называется проекцией и для него необходима матрица проекции. Я не буду обсуждать получение матрицы проекции, но на рис. 2.9 показана стандартная матрица перспективной проекции и указано назначение каждого из ее компонентов.
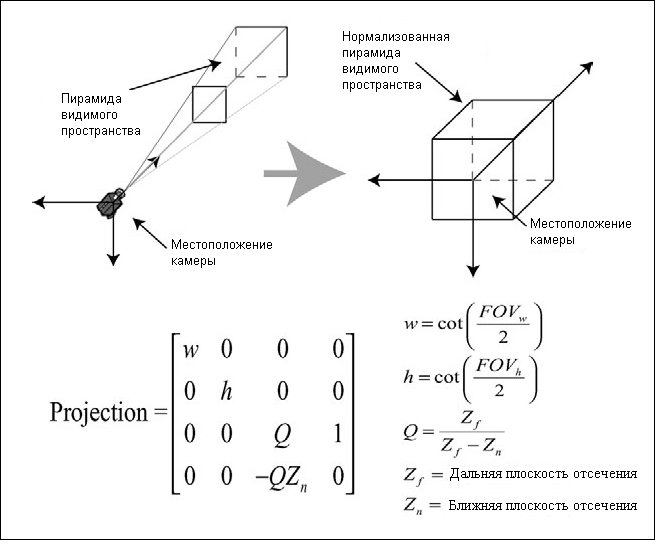
Рис. 2.9. Матрица проекции и ее компоненты
Формулы на рис. 2.9 могут показаться пугающими. Главное в них то, что компоненты w и h матрицы определяют ширину и высоту экрана в терминах поля зрения камеры (FOV), задавая размеры пирамиды видимого пространства для камеры. Компоненты Q и QZ матрицы определяют переднюю и заднюю плоскости отсечения камеры, задающие глубину области пространства, которая будет визуализироваться камерой.
Матрица проекции применяется к объектам точно так же, как и любое другое преобразование. Умножение этой матрицы на матрицу преобразования в пространство камеры нашего объекта дает нам матрицу преобразования в экранное пространство. Как видно на рис. 2.10, матрица преобразований объект-камера-экран получает объект, преобразует его и проецирует на экран.
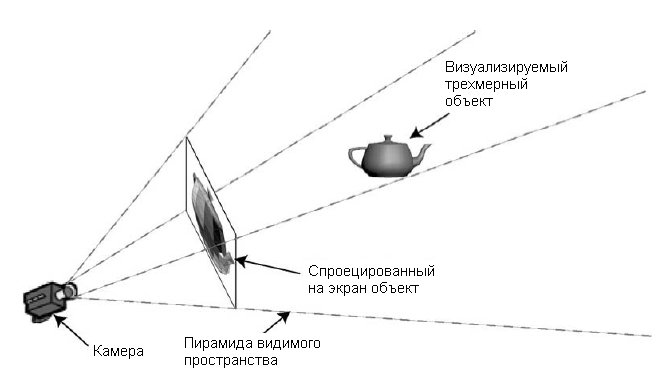
Рис. 2.10. Процесс проецирования объекта на экран с использованием матрицы проекции
Применив к нашим вершинам матрицу проекции, мы получаем представление геометрии, которое подходит для отображения на экране. Поскольку мы предполагаем, что объекты непрозрачны, в общем случае мы не можем видеть, что находится внутри них. Раз вы не можете видеть внутренние полигоны сетки, то и визуализировать их не надо. Большинство архитектур используют эту особенность, чтобы оптимизировать производительность визуализации путем удаления граней, направленных от камеры; это называется отбрасыванием обратных граней (back face culling). Направлен полигон к камере или от нее определяется по порядку следования его вершин — по часовой стрелке или против часовой стрелки; это называется порядком обхода (winding order) полигона.
После завершения оптимизации большинство визуализаторов также выполняют отсечение. У отсечения две главные задачи. Во-первых, оптимизируется процесс визуализации путем исключения тех полигонов, которые полностью находятся вне экрана. Во-вторых, полигоны, которые попадают на экран только частично, обрезаются по размеру экрана, чтобы уменьшить объем вычислений.
Теперь мы знаем, где полигон находится на экране и видим ли он, но нам все еще надо нарисовать что-нибудь на этом полигоне. Для этого в архитектуре визуализации используется операция называемая растеризацией (rasterizing). Мы знаем, в каком месте экрана будет находиться полигон, так что можем определить, какие пиксели экрана будет занимать объект. В процессе растеризации полигон обычно делится на горизонтальные линии пикселей, которые будут визуализированы. Для каждой линии визуализатор интерполирует информацию вершин (местоположение, цвет, координаты текстуры) с учетом ориентации полигона в трехмерном пространстве.
Теперь для каждого пикселя у нас есть вся необходимая для рисования информация. Однако в этот момент большинство визуализаторов выполняют еще одну оптимизацию, позволяющую предотвратить рисование лишних пикселей. Для каждого рисуемого на экране пикселя в Z-буфере сохраняется информация о его глубине. Этот Z-буфер отслеживает, какие пиксели визуализируемой сцены находятся ближе всего к камере. Для каждого нового пикселя (или фрагмента) выполняется сравнение значений Z-буфера, чтобы определить видим пиксель или он скрыт другими пикселями.
Если пиксель не скрыт другими пикселями, мы используем интерполяцию координат текстур и комбинируем результат с цветами вершин и другими данными вершины для отображения пикселя на экране. После определения итогового цвета, но перед выводом пикселя на экран, могут выполняться другие операции визуализации, такие как альфа-смешивание и проверка трафарета.
Намылить, прополоскать, повторить! Проделайте описанные выше операции для каждого пикселя каждого полигона, и вы получите визуализированную сцену. Помните, что это очень упрощенный краткий обзор того, как выполняется визуализация, но он должен дать вам достаточное представление о том, что происходит внутри вашей видеокарты. И как вы можете видеть, происходит очень многое! Позднее в этой главе вы узнаете, какое место во всем этом занимают вершинные и пиксельные шейдеры.
| netlib.narod.ru | < Назад | Оглавление | Далее > |