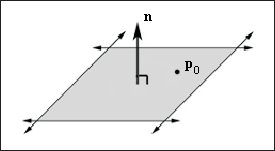
Рис. 11. Плоскость, заданная вектором нормали n и точкой плоскости p0
| netlib.narod.ru | < Назад | Оглавление | Далее > |
Плоскость описывается с помощью вектора n и принадлежащей плоскости точки p0. Вектор n называется вектором нормали (normal vector) плоскости и должен быть перпендикулярен плоскости (рис. 11).
 |
Рис. 11. Плоскость, заданная вектором нормали n и точкой плоскости p0 |
На рис. 12 мы видим, что графическим представлением плоскости является множество всех точек, удовлетворяющих условию

 |
Рис. 12. Если точка p0 принадлежит плоскости, то точка p также принадлежит этой плоскости в том случае, если вектор (p – p0) перпендикулярен вектору нормали плоскости |
При описании конкретной плоскости вектор нормали n и принадлежащая плоскости точка p0 обычно фиксированы, и формула (7) записывается в следующем виде:

где d = –n Ч p0.
Для представления плоскости в коде достаточно указать вектор нормали n и константу d. Можно думать об этом как о четырехмерном векторе, который мы будем обозначать (n, d). В библиотеке D3DX для плоскостей используется следующая структура:
typedef struct D3DXPLANE
{
#ifdef __cplusplus
public:
D3DXPLANE() {}
D3DXPLANE(CONST FLOAT*);
D3DXPLANE(CONST D3DXFLOAT16*);
D3DXPLANE(FLOAT a, FLOAT b, FLOAT c, FLOAT d);
// приведение типа
operator FLOAT* ();
operator CONST FLOAT* () const;
// унарные операторы
D3DXPLANE operator + () const;
D3DXPLANE operator - () const;
// бинарные операторы
BOOL operator == (CONST D3DXPLANE&) const;
BOOL operator != (CONST D3DXPLANE&) const;
#endif //__cplusplus
FLOAT a, b, c, d;
} D3DXPLANE, *LPD3DXPLANE;
где a, b, и c — это компоненты вектора нормали плоскости n, а d — это константа d из формулы (8).
Формула (8) в основном используется для проверки местоположения точки относительно плоскости. Предположим, нам дана плоскость (n, d), и мы хотим узнать как точка p расположена относительно этой плоскости:
Если n Ч p + d = 0, то точка p принадлежит плоскости.
Если n Ч p + d > 0, то точка p находится перед плоскостью в положительном полупространстве плоскости.
Если n Ч p + d < 0, то точка p находится за плоскостью в отрицательном полупространстве плоскости.
Приведенная ниже функция библиотеки D3DX вычисляет значение n Ч p + d для заданных плоскости и точки:
FLOAT D3DXPlaneDotCoord(
CONST D3DXPLANE *pP, // плоскость
CONST D3DXVECTOR3 *pV // точка
);
// Проверка местоположения точки относительно плоскости
D3DXPLANE p(0.0f, 1.0f, 0.0f, 0.0f);
D3DXVECTOR3 v(3.0f, 5.0f, 2.0f);
float x = D3DXPlaneDotCoord(&p, &v);
if( x приблизительно равно 0.0f ) // v принадлежит плоскости
if( x > 0 ) // v в положительном полупространстве
if( x < 0 ) // v в отрицательном полупространстве
Вместо непосредственного указания нормали и кратчайшего расстояния до начала координат, мы можем использовать еще два способа задания плоскостей. Зная вектор нормали n и принадлежащую плоскости точку p0 мы можем вычислить значение d следующим образом:

Для выполнения этих вычислений библиотека D3DX предоставляет следующую функцию:
D3DXPLANE *D3DXPlaneFromPointNormal(
D3DXPLANE* pOut, // Результат
CONST D3DXVECTOR3* pPoint, // Точка плоскости
CONST D3DXVECTOR3* pNormal // Нормаль плоскости
);
Кроме того, мы можем создать плоскость, указав три принадлежащие ей точки.
Имея три точки p0, p1, p2, мы можем сформировать два вектора плоскости:

Затем с помощью векторного произведения можно вычислить нормаль плоскости. Помните о правиле левой руки.

Следовательно, –(n Ч p0) = d.
Для создания плоскости по трем заданным точкам библиотека D3DX предоставляет следующую функцию:
D3DXPLANE *D3DXPlaneFromPoints(
D3DXPLANE* pOut, // Результат
CONST D3DXVECTOR3* pV1, // Первая точка плоскости
CONST D3DXVECTOR3* pV2, // Вторая точка плоскости
CONST D3DXVECTOR3* pV3 // Третья точка плоскости
);
Иногда может сложиться такая ситуация, что у нас есть плоскость и нам надо нормализовать ее вектор нормали. На первый взгляд нам достаточно нормализовать вектор нормали как любой другой вектор. Но вспомните, что в формуле n Ч p + d = 0 d = –n Ч p0. Как видите, длина вектора нормали влияет на константу d. Следовательно, если мы нормализуем вектор нормали, нам надо заново вычислить d. Обратите внимание, что

Следовательно, для нормализации вектора нормали плоскости (n, d) мы получаем следующую формулу:

Для нормализации вектора нормали плоскости можно использовать следующую функцию библиотеки D3DX:
D3DXPLANE *D3DXPlaneNormalize(
D3DXPLANE *pOut, // Нормализованная плоскость
CONST D3DXPLANE *pP // Исходная плоскость
);
Ленджел в своей книге «Mathematics for 3D Game Programming & Computer Graphics» показал, что мы можем преобразовать плоскость (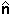 , d) представив ее как четырехмерный вектор и умножив на результат транспонирования инверсии описывающей желаемое преобразование матрицы. Обратите внимание, что перед этим необходимо нормализовать вектор нормали плоскости.
, d) представив ее как четырехмерный вектор и умножив на результат транспонирования инверсии описывающей желаемое преобразование матрицы. Обратите внимание, что перед этим необходимо нормализовать вектор нормали плоскости.
Для выполнения этих действий можно использовать следующую функцию библиотеки D3DX:
D3DXPLANE *D3DXPlaneTransform(
D3DXPLANE *pOut, // Результат
CONST D3DXPLANE *pP, // Исходная плоскость
CONST D3DXMATRIX *pM // Матрица преобразования
);
А вот пример кода:
D3DXMATRIX T(...); // Инициализация. T - требуемое преобразование D3DXMATRIX inverseOfT; D3DXMATRIX inverseTransposeOfT; D3DXMatrixInverse(&inverseOfT, 0, &T); D3DXMatrixTranspose(&inverseTransposeOfT, &inverseOfT); D3DXPLANE p(...); // Инициализация плоскости D3DXPlaneNormalize(&p, &p); // Нормализация вектора нормали D3DXPlaneTransform(&p, &p, &inverseTransposeOfT);
Пусть у нас есть точка p в трехмерном пространстве и нам необходимо найти точку q, принадлежащую плоскости (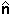 , d) и ближайшую к точке p. Обратите внимание: предполагается что вектор нормали плоскости нормализован, это упрощает решение задачи.
, d) и ближайшую к точке p. Обратите внимание: предполагается что вектор нормали плоскости нормализован, это упрощает решение задачи.
 |
Рис. 13. Точка q плоскости ( |
На рис. 13 видно, что q = p + (–k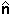 ), где k — это кратчайшее расстояние от точки p до плоскости, которое одновременно является и кратчайшим расстоянием между точками p и q. Помните, что если вектор нормали плоскости n нормализован, то n Ч p + d является кратчайшим расстоянием от плоскости до точки p.
), где k — это кратчайшее расстояние от точки p до плоскости, которое одновременно является и кратчайшим расстоянием между точками p и q. Помните, что если вектор нормали плоскости n нормализован, то n Ч p + d является кратчайшим расстоянием от плоскости до точки p.
| netlib.narod.ru | < Назад | Оглавление | Далее > |