
| netlib.narod.ru | < Назад | Оглавление | Далее > |
Создавая использующие Direct3D программы, для представления преобразований мы будем применять матрицы 4 × 4. Идея заключается в следующем: мы инициализируем элементы матрицы X размером 4 × 4 таким образом, чтобы они описывали требуемое преобразование. Затем мы помещаем координаты точки или компоненты вектора в столбцы вектора-строки v размером 1 × 4. Результатом произведения vX будет новый преобразованный вектор v'. Например, если матрица X представляет перемещение на 10 единиц вдоль оси X, и v = [2, 6, –3, 1], произведение vX = v' = [12, 6, –3, 1].
Следует пояснить несколько моментов. Мы используем матрицы размера 4 × 4 по той причине, что они позволяют представить все необходимые нам преобразования. На первый взгляд матрицы размером 3 × 3 кажутся более подходящими для трехмерной графики. Однако, с их помощью нельзя представить ряд преобразований, которые могут нам потребоваться, таких как перемещение, перспективная проекция и отражение. Помните, что мы работаем с произведением вектора на матрицу и при выполнении преобразований ограничены правилами умножения матриц. Дополнение матрицы до размера 4 × 4 позволяет нам с помощью матрицы описать большинство преобразований и при этом произведение вектора на матрицу будет определено.
Мы упомянули, что координаты точки или компоненты вектора будем хранить в столбцах вектора-строки размером 1 × 4. Но наши точки и векторы — трехмерные! Зачем же использовать вектор-строку 1 × 4? Мы должны дополнить наши трехмерные точки/векторы до четырехмерного вектора-строки 1 × 4 чтобы был определен результат умножения вектора на матрицу; произведение вектора-строки 1 × 3 и матрицы 4 × 4 не определено.
Так какое же значение использовать для четвертой компоненты, которую, кстати, мы будем обозначать w? Когда вектор-строка 1 × 4 используется для представления точки, значение w будет равно 1. Это позволяет корректно выполнять перемещение точки. Поскольку вектор не зависит от местоположения, операция перемещения векторов не определена и результат попытки переместить вектор не имеет смысла. Чтобы предотвратить перемещение векторов мы, помещая компоненты вектора в вектор-строку 1 × 4, присваиваем компоненте w значение 0. Например, точка p = (p1, p2, p3), помещенная в вектор-строку 1 × 4 будет выглядеть как [p1, p2, p3, 1], а вектор v = (v1, v2, v3), помещенный в вектор-строку 1 × 4 будет выглядеть как [v1, v2, v3, 0].
Иногда в результате преобразований компонента w вектора будет меняться таким образом, что w ≠ 0 и w ≠ 1. Взгляните на следующий пример:

для p3 ≠ 0 и p3 ≠ 1.
Обратите внимание, что w = p3. Когда w ≠ 0 и w ≠ 1, мы говорим, что у нас есть вектор в однородном пространстве (homogeneous space), в противоположность векторам в трехмерном пространстве. Мы можем отобразить вектор в однородном пространстве обратно на трехмерное пространство, разделив каждую компоненту вектора на значение компоненты w. Например, для отображения вектора (x, y, z, w) в однородном пространстве в трехмерный вектор x, выполним следующие операции:

Переход к однородному пространству и обратное отображение векторов в трехмерное пространство используются в программировании трехмерной графики для выполнения перспективной проекции.
 |
Рис. 8. Перемещение на 12 единиц по оси X и на –10 единиц по оси Y |
Мы можем переместить вектор (x, y, z, 1) на px единиц по оси Х, py единиц по оси Y и pz единиц по оси Z умножив его на следующую матрицу:

Для создания матрицы перемещения в библиотеке D3DX используется следующая функция:
D3DXMATRIX *D3DXMatrixTranslation(
D3DXMATRIX* pOut, // Результат
FLOAT x, // Количество единиц для перемещения по оси X
FLOAT y, // Количество единиц для перемещения по оси Y
FLOAT z // Количество единиц для перемещения по оси Z
);
| УПРАЖНЕНИЕ | Пусть T(p) — это матрица, представляющая преобразование перемещения и пусть v = [v1, v2, v3, 0] — это произвольный вектор. Проверьте, что vT(p) = v (то есть, что если w = 0, преобразование перемещения не влияет на вектор). |
|
Инверсия матрицы перемещения получается путем простой смены знака компонент вектора перемещения p.
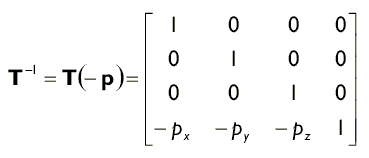
 |
Рис. 9. Поворот на 30 градусов против часовой стрелки вокруг оси Z |
Используя приведенные ниже матрицы мы можем повернуть вектор на φ радиан вокруг осей X, Y или Z. Обратите внимание, что если смотреть вдоль оси вращения по направлению к началу координат, то углы измеряются по часовой стрелке.
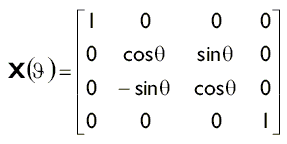
Для создания матрицы вращения вокруг оси X в библиотеке D3DX используется следующая функция:
D3DXMATRIX *D3DXMatrixRotationX(
D3DXMATRIX* pOut, // Результат
FLOAT Angle // Угол поворота в радианах
);

Для создания матрицы вращения вокруг оси Y в библиотеке D3DX используется следующая функция:
D3DXMATRIX *D3DXMatrixRotationY(
D3DXMATRIX* pOut, // Результат
FLOAT Angle // Угол поворота в радианах
);

Для создания матрицы вращения вокруг оси Z в библиотеке D3DX используется следующая функция:
D3DXMATRIX *D3DXMatrixRotationZ(
D3DXMATRIX* pOut, // Результат
FLOAT Angle // Угол поворота в радианах
);
Инверсией матрицы вращения R является результат транспонирования этой матрицы: RT = R-1. Такие матрицы называются ортогональными.
 |
Рис. 10. Масштабирование с коэффициентом 1/2 по оси X и коэффициентом 2 по оси Y |
Мы можем масштабировать вектор с коэффициентом qx по оси Х, коэффициентом qy по оси Y и коэффициентом qz по оси Z, умножив его на следующую матрицу:

Для создания матрицы масштабирования в библиотеке D3DX используется следующая функция:
D3DXMATRIX *D3DXMatrixScaling(
D3DXMATRIX* pOut, // Результат
FLOAT sx, // Коэффициент масштабирования по оси X
FLOAT sy, // Коэффициент масштабирования по оси Y
FLOAT sz // Коэффициент масштабирования по оси Z
);
Чтобы инвертировать матрицу масштабирования надо взять обратную дробь для каждого коэффициента масштабирования:

Часто мы будем применять к векторам целую последовательность преобразований. Например, мы можем масштабировать вектор, затем повернуть его и потом переместить в требуемую позицию.
В качестве примера мы рассмотрим вектор p = [5, 0, 0, 1], который масштабируем по всем осям с коэффициентом 1/5, затем повернем его на π/4 радиан вокруг оси Y и, наконец, переместим на 1 единицу по оси X, 2 единицы по оси Y и –3 единицы по оси Z.
Обратите внимание, что мы должны выполнить масштабирование, поворот вокруг оси Y и перемещение. Мы инициализируем наши матрицы преобразований S, Ry, T для масштабирования, поворота и перемещения соответственно, следующим образом:

Применив последовательность преобразований в заданном порядке — масштабирование, вращение, перемещение — получим:

Ключевым преимуществом использования матриц является возможность использования умножения матриц для комбинирования нескольких преобразований в одной матрице. Вернемся к примеру, рассматриваемому в начале данного раздела. Давайте с помощью умножения матриц скомбинируем все три матрицы преобразований в одну, которая будет представлять все три преобразования сразу. Обратите внимание, что порядок, в котором мы умножаем матрицы должен соответствовать порядку применения отдельных преобразований.

В результате получаем pQ = [1.707, 2, –3.707, 1].
Возможность комбинировать преобразования значительно увеличивает производительность. Представьте, что вам необходимо применить одну и ту же последовательность преобразований масштабирования, вращения и перемещения к большому набору векторов (это обычная задача в трехмерной компьютерной графике). Вместо того, чтобы применять к каждому вектору последовательность преобразований, как мы делали это в формуле (5), можно скомбинировать все три преобразования в одной матрице, как мы делали это в формуле (6). После этого остается только умножить каждый вектор на единственную матрицу, содержащую комбинацию всех трех преобразований. Благодаря этому количество выполняемых операций умножения вектора на матрицу значительно сокращается.
Библиотека D3DX предоставляет две функции для преобразования точек и векторов соответственно. Функция D3DXVec3TransformCoord используется для преобразования точек и предполагает, что четвертая компонента вектора равна 1. Функция D3DXVec3TransformNormal используется для преобразования векторов и предполагает, что четвертая компонента вектора равна 0.
D3DXVECTOR3 *D3DXVec3TransformCoord(
D3DXVECTOR3* pOut, // Результат
CONST D3DXVECTOR3* pV, // Преобразуемая точка
CONST D3DXMATRIX* pM // Матрица преобразования
);
D3DXMATRIX T(...); // инициализация матрицы преобразований
D3DXVECTOR3 p(...); // инициализация точки
D3DXVec3TransformCoord(&p, &p, &T); // преобразование точки
D3DXVECTOR3 *D3DXVec3TransformNormal(
D3DXVECTOR3 *pOut, // Результат
CONST D3DXVECTOR3 *pV, // Преобразуемый вектор
CONST D3DXMATRIX *pM // Матрица преобразования
);
D3DXMATRIX T(...); // инициализация матрицы преобразований
D3DXVECTOR3 v(...); // инициализация вектора
D3DXVec3TransformNormal(&v, &v, &T); // преобразование вектора
| netlib.narod.ru | < Назад | Оглавление | Далее > |