| netlib.narod.ru | < Назад | Оглавление | Далее > |
В качестве второго примера давайте напишем два вершинных шейдера, которые будут выполнять затенение и обвод контуров рисунка в мультипликационном стиле (рис. 17.2).
Рис. 17.2. (а) Объекты с затенением выполненным по мультипликационной технологии (обратите внимание на резкие переходы между оттенками) (б) Усиление эффекта достигается путем обведения силуэта объекта (в) Объекты, затеняемые с использованием стандартного рассеянного освещения
Мультипликационная визуализация подходит не для всех игр, например она будет лишней в реалистичной игре с видом от первого лица. С другой стороны, она может значительно улучшить атмоферу тех игр, где надо передать ощущения, возникающие при просмотре мультфильма. Кроме того, мультипликационная визуализация достаточно проста в реализации и замечательно подходит для демонстрации возможностей вершинных шейдеров.
Мы разделим мультипликационную визуализацию на два этапа.
Мультипликационные рисунки обычно имеют несколько уровней интенсивности затенения с резкими переходами от одного уровня к другому; мы будем ссылаться на такой способ как на мультипликационное затенение (cartoon shading). На рис. 17.2(а) видно, что для затенения сеток используются всего три уровня интенсивности (яркий, средний и темный) и переходы между оттенками явно выражены в отличие от рис. 17.2(в), где показан плавный переход от темного оттенка к светлому.
Также в мультфильмах обычно обводится силуэт объектов, как показано на рис. 17.2(б).
Оба этапа требуют собственных вершинных шейдеров.
Для реализации мультипликационного затенения мы воспользуемся методикой, описанной Ландером в статье «Shades of Disney: Opaquing a 3D World», опубликованной в выпуске журнала Game Developer Magazine за март 2000 года. Работает она следующим образом: мы создаем состоящую из оттенков серого текстуру, которая будет управлять яркостью и должна состоять из требуемого нам количества оттенков. На рис. 17.3 показана текстура, которая будет использоваться в данном примере.
 |
Рис. 17.3. Текстура затенения содержит используемые градации яркости. Обратите внимание на резкие переходы между оттенками и на то, что яркость оттенков увеличивается слева направо |
Затем в вершинном шейдере мы выполняем стандартные для рассеянного освещения вычисления, определяя с помощью скалярного произведения косинус угла между нормалью вершины 
и вектором света 
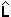, который используется для определения того, сколько света получает вершина:
Если s < 0, это значит, что угол между вектором света и нормалью вершины больше 90 градусов и, следовательно, поверхность не освещена. Поэтому, если s < 0, мы считаем что s = 0 и получаем значение s находящееся в диапазоне [0, 1].
Теперь в обычной модели рассеянного освещения мы использовали s для масштабирования цветового вектора, чтобы цвет становился темнее в зависимости от количества получаемого поверхностью света:
Однако, в результате мы получаем плавные переходы от светлых оттенков к темным. Это не то, что нам надо для мультипликационного затенения. Нам нужны четко выраженные переходы между несколькими оттенками (для мультипликационной визуализации хорошо подходит использование от двух до четырех оттенков).
Вместо того, чтобы использовать s для масштабирования цветового вектора, мы будем использовать его как координату текстуры u для текстуры затенения, о которой мы говорили раньше и показали на рис. 17.3.
В результате затенение вершин будет не плавным а резким. Например, текстура яркости может быть разделена на три оттенка, как показано на рис. 17.4.
 |
Рис. 17.4. Используемый оттенок зависит от интервала, в который попадает координата текстуры |
Тогда если значение s находится в диапазоне [0, 0.33] для затенения используется оттенок 0, если значение s находится в диапазоне (0.33, 0.66] — используется оттенок 1, и для значений s из диапазона (0.66, 1] используется оттенок 2. Естественно, переходы от одного оттенка к другому будут резкими, что нам и требуется.
Теперь мы представляем вершинный шейдер для мультипликационного затенения. Главной задачей шейдера является простое вычисление коэффициента s = 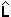Ч и установка соответствующих координат текстуры. Обратите внимание, что в выходную структуру мы добавили член данных для хранения вычисленных координат текстуры. Также заметьте, что мы по прежнему возвращаем цвет вершины, хотя не модифицируем его, а эффект затенения возникает, когда цвет вершины комбинируется с текстурой яркости.
// Файл: toon.txt
// Описание: Вершинный шейдер, выполняющий освещение объектов
// с созданием мультипликационного эффекта.
//
// Глобальные переменные
//
extern matrix WorldViewMatrix;
extern matrix WorldViewProjMatrix;
extern vector Color;
extern vector LightDirection;
static vector Black = {0.0f, 0.0f, 0.0f, 0.0f};
//
// Структуры
//
struct VS_INPUT
{
vector position : POSITION;
vector normal : NORMAL;
};
struct VS_OUTPUT
{
vector position : POSITION;
float2 uvCoords : TEXCOORD;
vector diffuse : COLOR;
};
//
// Точка входа
//
VS_OUTPUT Main(VS_INPUT input)
{
// Обнуляем члены выходной структуры
VS_OUTPUT output = (VS_OUTPUT)0;
// Преобразуем местположение вершины в однородное
// пространство отсечения
output.position = mul(input.position, WorldViewProjMatrix);
//
// Преобразуем вектор света и нормаль в пространство вида.
// Мы устанавливаем значение компоненты w равным нулю потому что
// мы преобразуем векторы. Предполагается, что в мировой матрице
// нет никакого масштабирования.
//
LightDirection.w = 0.0f;
input.normal.w = 0.0f;
LightDirection = mul(LightDirection, WorldViewMatrix);
input.normal = mul(input.normal, WorldViewMatrix);
//
// Вычисление одномерной координаты текстуры
// для мультипликационной визуализации
//
float u = dot(LightDirection, input.normal);
//
// Если u меньше нуля, считаем, что u равно нулю, поскольку
// отрицательные значения соответствуют углам между вектором света
// и нормалью большим 90 градусов. А если угол больше 90 градусов,
// значит поверхность не освещается
//
if(u < 0.0f)
u = 0.0f;
//
// Устанавливаем вторую координату текстуры на середину
//
float v = 0.5f;
output.uvCoords.x = u;
output.uvCoords.y = v;
// Сохраняем цвет
output.diffuse = Color;
return output;
}
И несколько комментариев:
Мы предполагаем, что в мировой матрице нет операций масштабирования поскольку в ином случае может измениться длинна и направление перемножаемых векторов.
Мы всегда устанавливаем координату текстуры v на середину текстуры. Это подразумевает, что мы используем только одну горизонтальную линию текстуры, а значит можем использовать одномерную текстуру яркости вместо двухмерной. Впрочем, программа нормально работает как с одномерными так и с двухмерными текстурами. В примере мы используем двухмерную текстуру, а не одномерную, но для этого нет никаких веских причин.
Чтобы усилить мультипликационный эффект, нам надо обвести силуэты объектов. Сделать это несколько сложнее, чем реализовать мультипликационное затенение.
Мы представляем край сетки в виде квадрата, образованного из двух треугольников (рис. 17.5).
 |
Рис. 17.5. Квадрат, представляющий край |
Мы выбрали квадрат по двум причинам: во-первых можно легко изменять толщину края просто меняя размеры квадрата, и во-вторых мы можем визуализировать вырожденные квадраты для скрытия отдельных краев, например, тех краев, которые не являются частью силуэта. В Direct3D мы создаем квадрат из двух треугольников. Вырожденный квадрат (degenerate quad) — это квадрат, созданный из двух вырожденных треугольников. Вырожденный треугольник (degenerate triangle) — это треугольник с нулевой площадью или, другими словами, треугольник у которого все три вершины лежат на одной прямой. Если передать вырожденный треугольник в конвейер визуализации, то ничего отображено не будет. Это очень полезно, поскольку если мы хотим скрыть какой-нибудь треугольник, достаточно просто сделать его вырожденным без действительного удаления из списка треугольников (буфера вершин). Вспомните, что нам надо отображать только края силуэта, а не все края сетки.
Когда мы впервые создаем край, то указываем его четыре вершины таким образом, чтобы квадрат был вырожденный (рис. 17.6), а это значит, что данный край будет скрыт (не будет отображаться при визуализации).
 |
Рис. 17.6. Вырожденный квадрат, описывающий край, разделенный на два треугольника |
Обратите внимание, что для двух вершин, v0 и v1 на рис. 17.6, мы указываем в качестве вектора нормали вершины нулевой вектор. Затем, когда мы передаем вершины края в вершинный шейдер, он проверяет, является ли данный край частью силуэта. Если да, вершинный шейдер смещает позицию вершин вдоль вектора нормали вершины на заданный скаляр. Обратите внимание, что те вершины, для которых указан нулевой вектор нормали, не смещаются. Таким образом мы получаем невырожденный квадрат, представляющий край силуэта, как показано на рис. 17.7.
 |
Рис. 17.7. Вершины v2 и v3 края силуэта смещаются в направлении их нормалей вершин n2 и n3 соответственно. Обратите внимание, что вершины v0 и v1 остаются на фиксированных позициях и никуда не смещаются, поскольку их векторы нормалей вершин — нулевые векторы. Благодаря этому происходит успешное восстановление квадрата, представляющего край силуэта |
Край является частью силуэта если он находится на стыке двух граней face0 и face1, и эти грани ориентированы в различных направлениях относительно вектора взгляда. То есть, если одна из граней является фронтальной, а другая — обратной, то край между ними является частью силуэта. На рис. 17.8 приведены примеры краев являющихся и не являющихся частью силуэта.
 |
Рис. 17.8. На рис. (a) одна из граней, совместно использующих край, образованный вершинами v0 и v1 является фронтальной, а другая — обратной, следовательно край является частью силуэта. На рис. (б) обе грани, совместно использующие край, образованный вершинами v0 и v1 являются фронтальными и, следовательно, край не является частью силуэта |
Из вышеприведенного материала следует, что для того, чтобы определить является ли вершина частью силуэта, нам надо знать векторы нормалей граней face0 и face1, к которым относится данная вершина. Это отражено в структуре данных вершины края:
struct VS_INPUT
{
vector position : POSITION;
vector normal : NORMAL0;
vector faceNormal1 : NORMAL1;
vector faceNormal2 : NORMAL2;
};
Первые два компонента мы уже обсуждали, но сейчас настало время взглянуть на два дополнительных вектора нормали — faceNormal1 и faceNormal2. Эти векторы являются нормалями тех двух граней на стыке которых находится рассматриваемый край, а именно face0 и face1.
Математическая часть проверки, является ли вершина частью силуэта, заключается в следующем. Предположим, мы находимся в пространстве вида. Пусть v — это вектор, направленный от начала координат до проверяемой вершины (рис. 17.8). Пусть n0 — это нормаль грани face0, а n1 — нормаль грани face1. Тогда вершина является частью силуэта, если следующее сравнение истино:
Выражение (1) истино если знаки результатов двух скалярных произведений различны, что делает левую часть формулы отрицательной. Вспомните свойства скалярного произведения — если знаки двух скалярных произведений различны, это значит, что одна грань фронтальная, а другая — обратная.
Теперь рассмотрим случай, когда край образован только одной гранью, как показано на рис. 17.9, чья нормаль хранится в faceNormal1.
 |
Рис. 17.9. Край, определенный вершинами v0 и v1 используется только одной гранью |
Мы считаем, что такие края всегда являются частью силуэта. Чтобы вершинный шейдер обрабатывал такие грани как часть силуэта, мы устанавливаем что faceNormal2 = -faceNormal1. таким образом, нормали граней будут направлены в разные стороны и формула (1) будет истинна, указывая, что край является частью силуэта.
Генерация краев сетки очень проста; мы перебираем грани сетки и для каждой стороны грани формируем квадрат (вырожденный, как показано на рис. 17.6).
Для вершин каждого края нам также необходимо знать две грани между которыми этот край находится. Одна из граней — это текущий треугольник. Например, если мы вычисляем край i-ой грани, то i-ая грань участвует в формировании края. Другую участвующую в формировании края грань можно найти с помощью данных о смежности граней сетки.
Настала пора представить код вершинного шейдера для визуализации силуэта. Основная задача шейдера заключается в определении того, является ли переданная вершина частью силуэта. Если да, то вершинный шейдер осуществляет сдвиг вершины на заданный скаляр в направлении вектора нормали вершины.
// Файл: outline.txt
// Описание: Вершинный шейдер, отображающий силуэт
//
// Глобальные переменные
//
extern matrix WorldViewMatrix;
extern matrix ProjMatrix;
static vector Black = {0.0f, 0.0f, 0.0f, 0.0f};
//
// Структуры
//
struct VS_INPUT
{
vector position : POSITION;
vector normal : NORMAL0;
vector faceNormal1 : NORMAL1;
vector faceNormal2 : NORMAL2;
};
struct VS_OUTPUT
{
vector position : POSITION;
vector diffuse : COLOR;
};
//
// Точка входа
//
VS_OUTPUT Main(VS_INPUT input)
{
// Обнуляем члены выходной структуры
VS_OUTPUT output = (VS_OUTPUT)0;
// Преобразуем местоположение в пространство вида
input.position = mul(input.position, WorldViewMatrix);
// Вычисляем вектор направления взгляда на вершину.
// Вспомните, что в пространстве вида зритель находится
// в начале координат (зритель это то же самое, что и камера).
vector eyeToVertex = input.position;
// Преобразуем нормали в пространство вида. Компоненте w
// присваиваем нуль, поскольку преобразуем векторы.
// Предполагается, что в мировой матрице нет масштабирования
input.normal.w = 0.0f;
input.faceNormal1.w = 0.0f;
input.faceNormal2.w = 0.0f;
input.normal = mul(input.normal, WorldViewMatrix);
input.faceNormal1 = mul(input.faceNormal1, WorldViewMatrix);
input.faceNormal2 = mul(input.faceNormal2, WorldViewMatrix);
// Вычисляем косинус угла между вектором eyeToVertex
// и нормалями граней
float dot0 = dot(eyeToVertex, input.faceNormal1);
float dot1 = dot(eyeToVertex, input.faceNormal2);
// Если у косинусов разные знаки (один положительный,
// а другой отрицательный) значит край является частью
// силуэта
if((dot0 * dot1) < 0.0f)
{
// Знаки разные, значит вершина является частью
// края силуэта, смещаем позиции вершин на заданный
// скаляр в направлении нормали вершины
input.position += 0.1f * input.normal;
}
// Преобразование в однородное пространство отсечения
output.position = mul(input.position, ProjMatrix);
// Устанавливаем цвет силуэта
output.diffuse = Black;
return output;
}
| netlib.narod.ru | < Назад | Оглавление | Далее > |