
| netlib.narod.ru | < Назад | Оглавление | Далее > |
После того, как мы сконструировали ландшафт, хорошо добавить возможность перемещать камеру таким образом, чтобы она имитировала ходьбу по ландшафту. То есть нам надо менять высоту камеры (координату Y) в зависимости от того, в каком месте ландшафта мы находимся. Для этого мы сначала должны определить по координатам X и Z камеры квадрат ландшафта в котором мы находимся. Все это делает функция Terrain::getHeight; в своих параметрах она получает координаты X и Z камеры и возвращает высоту, на которой должна быть расположена камера, чтобы она оказалась над ландшафтом. Давайте рассмотрим реализацию функции.
float Terrain::getHeight(float x, float z)
{
// Выполняем преобразование перемещения для плоскости XZ,
// чтобы точка START ландшафта совпала с началом координат.
x = ((float)_width / 2.0f) + x;
z = ((float)_depth / 2.0f) - z;
// Масштабируем сетку таким образом, чтобы размер
// каждой ее ячейки стал равен 1. Для этого используем
// коэффициент 1 / cellspacing поскольку
// cellspacing * 1 / cellspacing = 1.
x /= (float)_cellSpacing;
z /= (float)_cellSpacing;
Сперва мы выполняем перемещение в результате которого начальная точка ландшафта будет совпадать с началом координат. Затем мы выполняем операцию масштабирования с коэффициентом равным единице деленной на размер клетки; в результате размер клетки ландшафта будет равен 1. Затем мы переходим к новой системе координат, где положительное направление оси Z направлено «вниз». Конечно, вы не найдете кода меняющего систему координат, просто помните, что ось Z направлена вниз. Все эти этапы показаны на рис. 13.9.

Рис. 13.9. Исходная сетка ландшафта и сетка после переноса начальной точки ландшафта в начало координат, масштабирования, делающего размер квадрата равным 1 и смены направления оси Z
Мы видим, что измененная координатная система соответствует порядку элементов матрицы. То есть верхний левый угол — это начало координат, номера столбцов увеличиваются вправо, а номера строк растут вниз. Следовательно, согласно рис 13.9, и помня о том, что размер ячейки равен 1, мы сразу видим что номер строки и столбца для той клетки на которой мы находимся вычисляется так:
float col = ::floorf(x); float row = ::floorf(z);
Другими словами, номер столбца равен целой части координаты X, а номер строки — целой части координаты Z. Также вспомните, что результатом функции floor(t) является наибольшее целое число, которое меньше или равно t.
Теперь, когда мы знаем в какой ячейке находимся, можно получить высоты ее четырех вершин:
// A B // *---* // | / | // *---* // C D float A = getHeightmapEntry(row, col); float B = getHeightmapEntry(row, col+1); float C = getHeightmapEntry(row+1, col); float D = getHeightmapEntry(row+1, col+1);
Теперь мы знаем в какой ячейке находимся и высоты всех четырех ее вершин. Нам надо найти высоту (координату Y) точки ячейки с указанными координатами X и Z, где находится камера. Это нетривиальная задача, поскольку ячейка может быть наклонена, как показано на рис. 13.10.
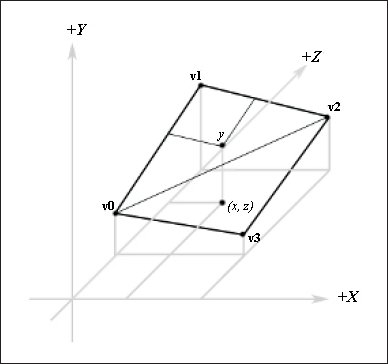 |
Рис. 13.10. Высота ячейки (координата Y) для заданных координат местоположения камеры X и Z |
Чтобы определить высоту мы должны узнать в каком треугольнике ячейки мы находимся. Вспомните, что каждая ячейка визуализируется как два треугольника. Чтобы определить в каком треугольнике мы находимся, мы берем тот квадрат сетки в котором находимся и перемещаем его таким образом, чтобы верхняя левая вершина совпадала с началом координат.
Поскольку переменные row и col определяют местоположение левой верхней вершины той ячейки где мы находимся, необходимо выполнить перемещение на –col по оси X и –row по оси Z. Преобразование координат X и Z выполняется так:
float dx = x - col; float dz = z - row;
Ячейка после выполнения преобразования показана на рис. 13.11.

Рис. 13.11. Ячейка до и после преобразования, переносящего ее верхнюю левую вершину в начало координат
Теперь, если dz < 1.0 – dx мы находимся в «верхнем» треугольнике Δv0v1v2. В ином случае мы находимся в «нижнем» треугольнике Δv0v2v3 (рис. 13.10).
Теперь мы посмотрим как определить высоту, если мы находимся в «верхнем» треугольнике. Для «нижнего» треугольника процесс аналогичен и ниже будет приведен код для обоих вариантов. Чтобы найти высоту когда мы находимся в «верхнем» треугольнике, надо сформировать два вектора u = (cellSpacing, B – A, 0) и v = (0, C – A, –cellSpacing), совпадающих со сторонами треугольника и начинающихся в точке, заданной вектором q = (qx, A, qz), как показано на рис. 13.12(а) Затем мы выполняем линейную интерполяцию вдоль вектора u на dx и вдоль вектора v на dz. Эти интерполяции показаны на рис. 13.12(б). Координата Y вектора (q + dxu + dzv) дает нам высоту для заданных координат X и Z; чтобы увидеть, как это происходит, вспомните геометрическую интерпретацию сложения векторов.

Рис. 13.12. (а) Вычисляем два вектора, совпадающих со сторонами треугольника. (б) Высота вычисляется путем линейной интерполяции u на dx и v на dz
Обратите внимание, что поскольку нас интересует только значение высоты, мы можем выполнять интерполяцию только для компоненты y и игнорировать остальные компоненты. В этом случае высота определяется по формуле A + dxuy + dzvy.
Итак, вот заключительная часть кода метода Terrian::getHeight:
if(dz < 1.0f - dx) // верхний треугольник ABC
{
float uy = B - A; // A->B
float vy = C - A; // A->C
height = A + d3d::Lerp(0.0f, uy, dx) +
d3d::Lerp(0.0f, vy, dz);
}
else // нижний треугольник DCB
{
float uy = C - D; // D->C
float vy = B - D; // D->B
height = D + d3d::Lerp(0.0f, uy, 1.0f - dx) +
d3d::Lerp(0.0f, vy, 1.0f - dz);
}
return height;
}
Функция Lerp выполняет линейную интерполяцию вдоль одномерной линии и ее реализация выглядит так:
float d3d::Lerp(float a, float b, float t)
{
return a - (a*t) + (b*t);
}
| netlib.narod.ru | < Назад | Оглавление | Далее > |