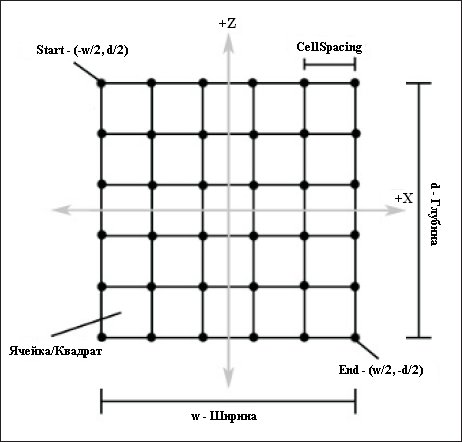
Рис. 13.4. Свойства размеченной треугольной сетки. Точки на пересечении линий сетки обозначают вершины
| netlib.narod.ru | < Назад | Оглавление | Далее > |
 |
Рис. 13.4. Свойства размеченной треугольной сетки. Точки на пересечении линий сетки обозначают вершины |
Рис. 13.4 иллюстрирует свойства ландшафта, термины и специальные точки, на которые мы будем ссылаться. Размер ландшафта определяется путем указания количества вершин в строке, количества вершин в столбце и размера ячейки. Все эти значения мы передаем в класс Terrain. Кроме того, мы передаем указатель на связанное с ландшафтом устройство, строку с именем файла, содержащего карту высот и коэффициент масштабирования, используемый при масштабировании элементов карты высот.
class Terrain
{
public:
Terrain(
IDirect3DDevice9* device,
std::string heightmapFileName,
int numVertsPerRow,
int numVertsPerCol,
int cellSpacing, // расстояние между вершинами
float heightScale); // коэффициент масштабирования высоты
... методы пропущены
private:
...устройство, буфер вершин и т.п. пропущены
int _numVertsPerRow;
int _numVertsPerCol;
int _cellSpacing;
int _numCellsPerRow;
int _numCellsPerCol;
int _width;
int _depth;
int _numVertices;
int _numTriangles;
float _heightScale;
};
Чтобы увидеть объявление класса Terrain полностью, посмотрите исходный код примера в сопроводительных файлах; оно слишком велико, чтобы приводить его в тексте.
На основании переданных конструктору данных мы вычисляем другие параметры ландшафта:
_numCellsPerRow = _numVertsPerRow - 1; _numCellsPerCol = _numVertsPerCol - 1; _width = _numCellsPerRow * _cellSpacing; _depth = _numCellsPerCol * _cellSpacing; _numVertices = _numVertsPerRow * _numVertsPerCol; _numTriangles = _numCellsPerRow * _numCellsPerCol * 2;
Кроме того, мы объявляем структуру вершин ландшафта следующим образом:
struct TerrainVertex
{
TerrainVertex(){}
TerrainVertex(float x, float y, float z, float u, float v)
{
_x = x; _y = y; _z = z; _u = u; _v = v;
}
float _x, _y, _z;
float _u, _v;
static const DWORD FVF;
};
const DWORD Terrain::TerrainVertex::FVF = D3DFVF_XYZ | D3DFVF_TEX1;
Обратите внимание, что TerrainVertex — это вложенный класс, объявленный внутри класса Terrain. Мы выбрали такую реализацию по той причине, что класс TerrainVertex не нужен вне класса Terrain.
Во время последующего обсуждения смотрите на рис. 13.4. Чтобы создать вершины нашей сетки мы просто начинаем генерировать данные вершин с той, которая отмечена на рисунке словом start и заполняем вершины ряд за рядом, пока не дойдем до той, которая отмечена словом end; при этом расстояние между вершинами задается параметром cellSpacing. Это позволяет нам получить координаты X и Z, но как насчет координаты Y? Координата Y берется из соответствующего элемента загруженной карты высот.
При вычислении координат текстуры, учитывая рис. 13.5, получаем простой сценарий, определяющий соответствие координат текстуры (u, v) вершине ландшафта (i, j) по следующей формуле:

где

 |
Рис. 13.5. Соответствие между вершинами ландшафта и координатами текстур |
И, в заключение, приведем код генерации данных вершин:
bool Terrain::computeVertices()
{
HRESULT hr = 0;
hr = _device->CreateVertexBuffer(
_numVertices * sizeof(TerrainVertex),
D3DUSAGE_WRITEONLY,
TerrainVertex::FVF,
D3DPOOL_MANAGED,
&_vb,
0);
if(FAILED(hr))
return false;
// координаты, с которых начинается генерация вершин
int startX = -_width / 2;
int startZ = _depth / 2;
// координаты, на которых завершается генерация вершин
int endX = _width / 2;
int endZ = -_depth / 2;
// вычисляем приращение координат текстуры
// при переходе от одной вершины к другой.
float uCoordIncrementSize = 1.0f / (float)_numCellsPerRow;
float vCoordIncrementSize = 1.0f / (float)_numCellsPerCol;
TerrainVertex* v = 0;
_vb->Lock(0, 0, (void**)&v, 0);
int i = 0;
for(int z = startZ; z >= endZ; z -= _cellSpacing)
{
int j = 0;
for(int x = startX; x <= endX; x += _cellSpacing)
{
// вычисляем правильный индекс в буфере вершин
// и карте высот на основании счетчиков вложенных циклов
int index = i * _numVertsPerRow + j;
v[index] = TerrainVertex(
(float)x,
(float)_heightmap[index],
(float)z,
(float)j * uCoordIncrementSize,
(float)i * vCoordIncrementSize);
j++; // следующий столбец
}
i++; // следующая строка
}
_vb->Unlock();
return true;
}
Чтобы вычислить индексы сетки мы просто в цикле перебираем все ее квадраты, начиная с верхнего левого и заканчивая правым нижним, как показано на рис. 13.4, и формируем два треугольника, образующие квадрат.
 |
Рис. 13.6. Вершины квадрата |
Главным трюком здесь является общая формула, позволяющая вычислить индексы треугольников, образующих квадрат в позиции (i, j). Рис. 13.6 позволяет вывести общую формулу для квадрата(i, j):
ΔABC = { i*numVertsPerRow + j,
i*numVertsPerRow + j + 1,
(i + 1)*numVertsPerRow + j }
ΔCBD = { (i + 1)*numVertsPerRow + j,
i*numVertsPerRow + j + 1,
(i + 1)*numVertsPerRow + j + 1 }
Вот код генерации индексов:
bool Terrain::computeIndices()
{
HRESULT hr = 0;
hr = _device->CreateIndexBuffer(
_numTriangles * 3 * sizeof(WORD), // 3 индекса на треугольник
D3DUSAGE_WRITEONLY,
D3DFMT_INDEX16,
D3DPOOL_MANAGED,
&_ib,
0);
if(FAILED(hr))
return false;
WORD* indices = 0;
_ib->Lock(0, 0, (void**)&indices, 0);
// Индекс, с которого начинается группа из 6 индексов,
// описывающая два треугольника, образующих квадрат
int baseIndex = 0;
// В цикле вычисляем треугольники для каждого квадрата
for(int i = 0; i < _numCellsPerCol; i++)
{
for(int j = 0; j < _numCellsPerRow; j++)
{
indices[baseIndex] = i * _numVertsPerRow + j;
indices[baseIndex + 1] = i * _numVertsPerRow + j + 1;
indices[baseIndex + 2] = (i+1) * _numVertsPerRow + j;
indices[baseIndex + 3] = (i+1) * _numVertsPerRow + j;
indices[baseIndex + 4] = i * _numVertsPerRow + j + 1;
indices[baseIndex + 5] = (i+1) * _numVertsPerRow + j + 1;
// следующий квадрат
baseIndex += 6;
}
}
_ib->Unlock();
return true;
}
| netlib.narod.ru | < Назад | Оглавление | Далее > |