5.3. Нормали вершин

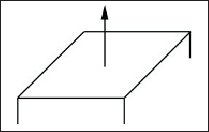
Нормалью грани (face normal) называется вектор, определяющиий ориентацию лицевой грани многоугольника (рис. 5.1).

Рис. 5.1. Лицевая нормаль поверхности

Нормали вершин (vertex normals) основаны на той же самой идее, но в этом случае задается не нормаль для всего многоугольника, а отдельная нормаль для каждой образующей его вершины (рис. 5.2).

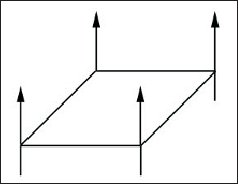Рис. 5.2. Нормали вершин поверхности

Direct3D необходимо знать нормали вершин, поскольку они необходимы чтобы оперделить под каким углом свет падает на грань. Кроме того, поскольку вычисление освещенности выполняется для каждой из вершин, Direct3D необходимо знать ориентацию грани (нормаль) для каждой вершины. Обратите внимание, что нормаль вершины не всегда совпадает с нормалью грани. Наиболее распростарненным примером объекта у которого нормали треугольных граней не совпадают с нормалями вершин является сфера или цилиндр (рис. 5.3).

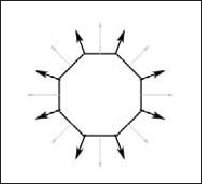Рис. 5.3. Пример объекта, у которого нормали вершин не совпадают с нормалями граней. Векторы нормалей вершин выделены черным цветом, а векторы нормалей граней — серым

Для описания нормалей вершин нам необходимо добавить соответствующие члены в структуру данных вершины:

struct Vertex
{
     float _x, _y, _z;
     float _nx, _ny, _nz;
     static const DWORD FVF;
}
const DWORD Vertex::FVF = D3DFVF_XYZ | D3DFVF_NORMAL;

Обратите внимание, что мы убрали члены данных, задающие цвет вершины, которые использовали в предыдущей главе. Дело в том, что теперь для вычисления цвета вершин мы будем использовать данные освещения.

Для простых объектов, таких как кубы и сферы, нормали вершин можно оперделить путем осмотра. Для сложных сеток необходим более алгоритмизированный способ. Предположим, что треугольник образован вершинами p₀, p₁ и p₂, и нам необходимо вычислить нормали n₀, n₁ и n₂ для каждой из вершин.

Простейший подход заключается в том, чтобы вычислить нормаль грани для треугольника и использовать ее в качестве нормали для всех трех вершин. Сперва вычислим два вектора, лежащих в полскости треугольника:

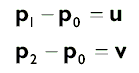
Тогда нормаль грани вычисляется по формуле:

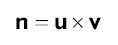
Поскольку нормаль каждой вершины совпадает с нормалью грани:

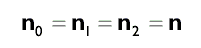
Ниже приведена функция, которая вычисляет нормаль треугольной грани на основании координат трех ее вершин. Обратите внимание, что функция предполагает, что вершины перечислены по часовой стрелке. Если это не так, нормаль будет указывать в противоположном направлении.

void ComputeNormal(D3DXVECTOR3* p0,
                   D3DXVECTOR3* p1,
                   D3DXVECTOR3* p2,
                   D3DXVECTOR3* out)
{
     D3DXVECTOR3 u = *p1 - *p0;
     D3DXVECTOR3 v = *p2 - *p0;

     D3DXVec3Cross(out, &u, &v);
     D3DXVec3Normalize(out, out);
}

Использование нормали грани в качестве нормалей вершин не позволяет добиться гладкого изображения состоящих из треугольных граней сложных кривых поверхностей. Лучшим методом вычисления нормалей вершин является усреднение нормалей (normal averaging). Чтобы вычислить вектор нормали v_n для вершины v, мы вычисляем нормали граней всех треугольников сетки, в которые входит данная вершина v. Затем вектор нормали вершины v_n получается путем вычисления среднего значения всех этих нормалей граней. Давайте разберем конкретный пример. Предположим, вершина v входит в три треугольника, для которых известны их нормали граней n₀, n₁ и n₂. Тогда v_n вычисляется путем усреднения нормалей граней:

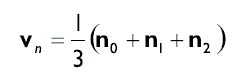
В процессе преобразований может получиться так, что векторы нормалей станут денормализованными. Так что лучше всего предусмотреть возможность подобной ситуации и приказать Direct3D заново нормализовать все векторы нормалей после преобразований, включив режим визуализации D3DRS_NORMALIZENORMALS:

Device->SetRenderState(D3DRS_NORMALIZENORMALS, true);