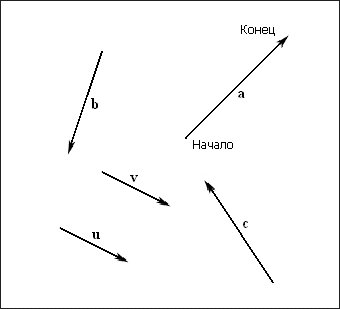
Рис. 1. Свободные векторы, определенные независимо от системы координат
| netlib.narod.ru | < Назад | Оглавление | Далее > |
Геометрическим представлением вектора является направленный отрезок прямой линии, что показано на рис. 1. У каждого вектора есть два свойства: длина (также называемая модулем или нормой вектора) и направление. Благодаря этому векторы очень удобны для моделирования физических величин, которые характеризуются модулем и направлением. Например, в главе 14 мы реализуем систему частиц. При этом мы будем использовать векторы для моделирования скорости и ускорения наших частиц. С другой стороны, в трехмерной компьютерной графике векторы часто используются только для моделирования направления. Например, нам часто требуется указать направление распространения световых лучей, ориентацию грани или направление камеры, глядящей на трехмерный мир. Векторы обеспечивают удобный механизм задания направления в трехмерном пространстве.
 |
Рис. 1. Свободные векторы, определенные независимо от системы координат |
Поскольку местоположение не является характеристикой вектора, два вектора с одинаковой длиной и указывающие в одном и том же направлении считаются равными, даже если они расположены в различных местах. Обратите внимание, что два таких вектора будут параллельны друг другу. Например, на рис. 1 векторы u и v равны.
На рис. 1 видно, что обсуждние векторов может вестись без упоминания системы координат, поскольку всю значимую информацию, — длину и направление, — вектор содержит в себе. Добавление системы координат не добавляет информации в вектор; скорее можно говорить, что вектор, значения которого являются его неотъемлимой частью, просто описан относительно конкретной системы координат. И если мы изменим систему координат, мы только опишем тот же самый вектор относительно другой системы.
Отметив этот важный момент, мы перейдем к изучению того, как векторы описываются в левосторонней трехмерной декартовой системе координат. На рис. 2 показаны левосторонняя и правосторонняя системы координат. Различие между ними — положительное направление оси Z. В левосторонней системе координат положительное направление оси Z погружается в страницу. В правосторонней системе координат положительное направление оси Z направлено от страницы.
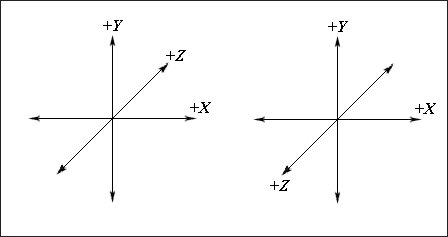 |
Рис. 2. Слева изображена левосторонняя система координат. Обратите внимание, что положительное направление оси Z направлено вглубь страницы. Справа изображена правостороняя система координат. Здесь положительное направление оси Z направлено от страницы |
Поскольку местоположение вектора не изменяет его свойств, мы можем перенести векторы таким образом, чтобы начало каждого из них совпадало с началом координат выбранной координатной системы. Когда начало вектора совпадает с началом координат, говорят, что вектор находится в стандартной позиции. Таким образом, если вектор находится в стандартной позиции, мы можем описать его, указав только координаты конечной точки. Мы будем называть эти координаты компонентами вектора. На рис. 3 показаны векторы, изображенные на рис. 1, которые были перемещены в стандартные позиции.
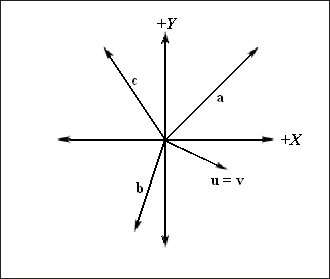 |
Рис. 3. Векторы в стандартной позиции, определенные в указанной системе координат. Обратите внимание, что векторы u и v полностью совпадают друг с другом потому что они равны |
Мы будем пользоваться для обозначения векторов полужирными строчными буквами, но иногда будем применять и полужирные заглавные буквы. Вот пример двух-, трех- и четырехмерных векторов соответственно: u = (ux, uy), N = (Nx, Ny, Nz), c = (cx, cy, cz, cw).
Теперь мы введем четыре специальных трехмерных вектора, которые показаны на рис. 4. Первый из них называется нулевым вектором, и значения всех его компонент равны нулю; мы будем обозначать такой вектор выделенным полужирным шрифтом нулем: 0 = (0, 0, 0). Следующие три специальных вектора называются единичными базовыми векторами (базовыми ортами) трехмерной системы координат. Эти векторы, направленные вдоль осей X, Y и Z нашей координатной системы, мы будем называть i, j и k соответственно. Модуль этих векторов равен единице, а определение выглядит следующим образом: i = (1, 0, 0), j = (0, 1, 0), k = (0, 0, 1).
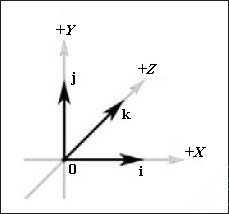 |
Рис. 4. Нулевой вектор и базовые орты трехмерной системы координат |
В библиотеке D3DX для представления векторов в трехмерном пространстве мы можем воспользоваться классом D3DXVECTOR3. Его определение выглядит следующим образом:
typedef struct D3DXVECTOR3 : public D3DVECTOR {
public:
D3DXVECTOR3() {};
D3DXVECTOR3( CONST FLOAT * );
D3DXVECTOR3( CONST D3DVECTOR& );
D3DXVECTOR3( FLOAT x, FLOAT y, FLOAT z );
// приведение типа
operator FLOAT* ();
operator CONST FLOAT* () const;
// операторы присваивания
D3DXVECTOR3& operator += ( CONST D3DXVECTOR3& );
D3DXVECTOR3& operator -= ( CONST D3DXVECTOR3& );
D3DXVECTOR3& operator *= ( FLOAT );
D3DXVECTOR3& operator /= ( FLOAT );
// унарные операторы
D3DXVECTOR3 operator + () const;
D3DXVECTOR3 operator - () const;
// бинарные операторы
D3DXVECTOR3 operator + ( CONST D3DXVECTOR3& ) const;
D3DXVECTOR3 operator - ( CONST D3DXVECTOR3& ) const;
D3DXVECTOR3 operator * ( FLOAT ) const;
D3DXVECTOR3 operator / ( FLOAT ) const;
friend D3DXVECTOR3 operator * ( FLOAT,
CONST struct D3DXVECTOR3& );
BOOL operator == ( CONST D3DXVECTOR3& ) const;
BOOL operator != ( CONST D3DXVECTOR3& ) const;
} D3DXVECTOR3, *LPD3DXVECTOR3;
Обратите внимание, что D3DXVECTOR3 наследует компоненты от D3DVECTOR, определение которого выглядит следующим образом:
typedef struct _D3DVECTOR {
float x;
float y;
float z;
} D3DVECTOR;
Так же, как и у скалярных величин, у векторов есть собственная арифметика, что видно из наличия описаний математических операций в определении класса D3DXVECTOR3. Возможно, сейчас вы не знаете, что делают эти методы. В следующих подразделах мы рассмотрим эти операции с векторами, другие вспомогательные функции работы с векторами из библиотеки D3DX и некоторые важные особенности обработки векторов.
В геометрии два вектора считаются равными, если они указывают в одном и том же направлении и имеют одинаковую длину. В алгебре говорят, что векторы равны, если у них одинаковое количество измерений и их соответствующие компоненты равны. Например, (ux, uy, uz) = (vx, vy, vz) если ux = vx, uy = vy и uz = vz.
В коде мы можем проверить равны ли два вектора, используя перегруженный оператор равенства:
D3DXVECTOR u(1.0f, 0.0f, 1.0f); D3DXVECTOR v(0.0f, 1.0f, 0.0f); if( u == v ) return true;
Аналогичным образом, можно убедиться, что два вектора не равны, используя перегруженный оператор неравенства:
if( u != v ) return true;
const float EPSILON = 0.001f;
bool Equals(float lhs, float rhs)
{
// если lhs == rhs разность должна быть равна нулю
return fabs(lhs - rhs) < EPSILON ? true : false;
}
Об этом не надо беспокоиться, работая с классом D3DXVECTOR, поскольку перегруженные операции сравнения все сделают за нас, но очень важно знать об этой особенности сравнения чисел с плавающей точкой.В геометрии модулем вектора называется длина направленного отрезка линии. В алгебре, зная компоненты вектора мы можем вычислить его модуль по следующей формуле:
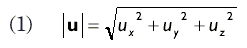
Вертикальные линии в |u| обозначают модуль u.
| ПРИМЕР | Вычислите модуль векторов u = (1, 2, 3) и v = (1, 1). РешениеДля вектора u мы получаем: 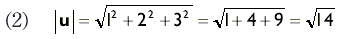 Обобщив формулу (1) для двухмерного пространства, для вектора v мы получим: 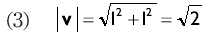 |
|
Работая с библиотекой D3DX, для вычисления модуля вектора мы можем применять следующую функцию:
FLOAT D3DXVec3Length( // Возвращает модуль
CONST D3DXVECTOR3* pV // Вектор, чью длину мы вычисляем
);
D3DXVECTOR3 v(1.0f, 2.0f, 3.0f);
float magnitude = D3DXVec3Length(&v); // = sqrt(14)
В результате нормализации получается вектор, направление которого совпадает с исходным, а модуль равен единице (единичный вектор). Чтобы нормализовать произвольный вектор, достаточно разделить каждый компонент вектора на модуль вектора, как показано ниже:
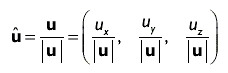
Мы отмечаем единичный вектор, помещая над его обозначением символ ^: û.
| ПРИМЕР | Нормализуйте векторы u = (1, 2, 3) и v = (1, 1). РешениеИз приведенных выше формул (2) и (3) мы знаем, что |u| = √14 и |v| = √2, поэтому: 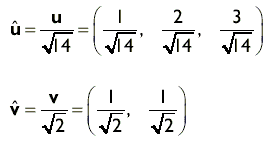 |
|
В библиотеке D3DX для нормализации векторов применяется следующая функция:
D3DXVECTOR3 *D3DXVec3Normalize(
D3DXVECTOR3* pOut, // Результат
CONST D3DXVECTOR3* pV // Нормализуемый вектор
);
Мы можем сложить два вектора, сложив их соответствующие компоненты; обратите внимание, что размерность складываемых векторов должна быть одинаковой:
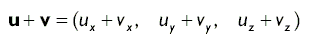
Геометрическая интерпретация сложения векторов показана на рис. 5.
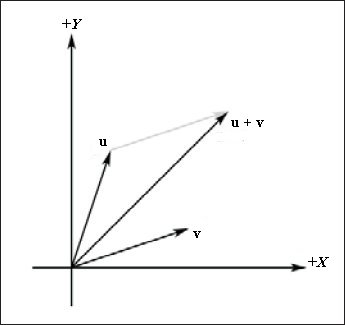 |
Рис. 5. Сложение векторов. Обратите внимание, как мы выполняем параллельный перенос вектора v таким образом, чтобы его начало совпало с концом вектора u; суммой будет вектор начало которого совпадает с началом вектора u, а конец совпадает с концом перенесенного вектора v |
В коде для сложения двух векторов мы будем применять перегруженый оператор сложения:
D3DXVECTOR3 u(2.0f, 0.0f, 1.0f); D3DXVECTOR3 v(0.0f, -1.0f, 5.0f); // (2.0 + 0.0, 0.0 + (-1.0), 1.0 + 5.0) D3DXVECTOR3 sum = u + v; // = (2.0f, -1.0f, 6.0f)
Аналогично сложению, вычитание векторов осуществляется путем вычитания их отдельных компонент. Опять же оба вектора должны иметь одинаковую размерность.
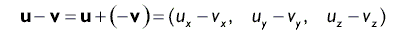
Геометрическая интерпретация вычитания векторов показана на рис. 6.
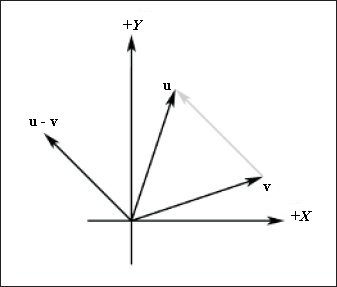 |
Рис. 6. Вычитание векторов |
В коде для вычитания двух векторов мы будем применять перегруженый оператор вычитания:
D3DXVECTOR3 u(2.0f, 0.0f, 1.0f); D3DXVECTOR3 v(0.0f, -1.0f, 5.0f); D3DXVECTOR3 difference = u - v; // = (2.0f, 1.0f, -4.0f)
Как видно на рис. 6, операция вычитания векторов возвращает вектор, начало которого совпадает с концом вектора v, а конец — с концом вектора u. Если мы интерпретируем компоненты u и v как координаты точек, то результатом вычитания будет вектор, направленный от одной точки к другой. Это очень удобная операция, поскольку нам часто будет необходимо найти вектор, описывающий направление от одной точки к другой.
Как видно из названия раздела, мы можем умножать вектор на скаляр, в результате чего происходит масштабирование вектора. Если масштабный множитель положителен, направление вектора не меняется. Если же множитель отрицателен, то направление вектора изменяется на противоположное (инвертируется).
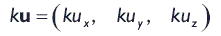
Класс D3DXVECTOR3 предоставляет оператор умножения вектора на скаляр:
D3DXVECTOR3 u(1.0f, 1.0f, -1.0f); D3DXVECTOR3 scaledVec = u * 10.0f; // = (10.0f, 10.0f, -10.0f)
Скалярное произведение векторов — это первая из двух определенных в векторной алгебре операций умножения. Вычисляется такое произведение следующим образом:
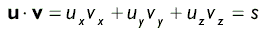
У приведенной выше формулы нет очевидной геометрической интерпретации. Используя теорему косинусов 1, мы получим отношение uЧv = |u||v|cos j, говорящее, что скалярное произведение двух векторов равно произведению косинуса угла между векторами на модули векторов. Следовательно, если u и v — единичные векторы, их скалярное произведение равно косинусу угла между ними.
Вот некоторые полезные свойства скалярного произведения:
Для вычисления скалярного произведения двух векторов в библиотеке D3DX предназначена следующая функция:
FLOAT D3DXVec3Dot( // Возвращает результат.
CONST D3DXVECTOR3* pV1, // Левый операнд.
CONST D3DXVECTOR3* pV2 // Правый операнд.
);
D3DXVECTOR3 u(1.0f, -1.0f, 0.0f);
D3DXVECTOR3 v(3.0f, 2.0f, 1.0f);
// 1.0*3.0 + -1.0*2.0 + 0.0*1.0
// = 3.0 + -2.0
float dot = D3DXVec3Dot(&u, &v); // = 1.0
Второй формой операции умножения, определенной в векторной алгебре, является векторное произведение. В отличие от скалярного произведения, результатом которого является число, результатом векторного произведения будет вектор. Векторным произведением двух векторов u и v будет другой вектор, p, являющийся взаимно перпендикулярным для векторов u и v. Это означает, что вектор p перпендикулярен вектору u и одновременно вектор p перпендикулярен вектору v.
Вычисляется векторное произведение по следующей формуле:
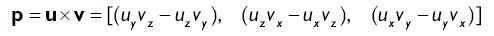
В компонентной форме вычисление выглядит так:
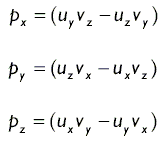
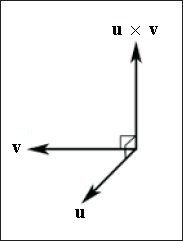 |
Рис. 7. Векторное произведение. Вектор p = u × v перпендикулярен как вектору u, так и вектору v |
| ПРИМЕР | Вычислите j = k × i = (0, 0, 1) × (1, 0, 0) и проверьте, что вектор j перпендикулярен как вектору i, так и вектору k. Решение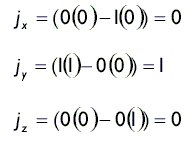 Таким образом, j = (0, 1, 0). Вспомните, в предыдущем разделе «Скалярное произведение векторов» говорилось, что если u Ч v = 0, значит u ^ v. Поскольку j Ч k = 0 и j Ч i = 0, мы знаем что вектор j перпендикулярен как вектору k, так и вектору i. |
|
Для вычисления векторного произведения двух векторов в библиотеке D3DX предназначена следующая функция:
D3DXVECTOR3 *D3DXVec3Cross(
D3DXVECTOR3* pOut, // Результат
CONST D3DXVECTOR3* pV1, // Левый операнд
CONST D3DXVECTOR3* pV2 // Правый операнд
);
Как явствует из рис. 7, вектор –p также взаимно перпендикулярен векторам u и v. Какой из векторов, p или –p будет возвращен в качестве результата векторного произведения определяется порядком операндов. Другими словами, u × v = –(v × u). Это заначит, что операция векторного произведения не является коммутативной. Определить, какой вектор будет возвращен в качестве результата, можно с помощью правила левой руки. (Мы используем правило левой руки, поскольку работаем с левосторонней системой координат. Если бы у нас была правосторонняя система координат, пришлось бы воспользоваться правилом правой руки.) Если расположить пальцы левой руки вдоль первого вектора, а ладонь руки — вдоль второго, отогнутый на 90 градусов большой палец укажет направление результирующего вектора.
1 Теорема косинусов определяет зависимость между сторонами и углами треугольника. Она утверждает, что во всяком треугольнике квадрат длины стороны равен сумме квадратов двух других сторон без удвоенного произведения длин этих сторон на косинус угла между ними. Если угол прямой, то теорема косинусов переходит в теорему Пифагора, т.к. косинус прямого угла равен 0.
| netlib.narod.ru | < Назад | Оглавление | Далее > |